【题目】如下一组数:![]() ,请用你发现的规律,猜想第2018个数为____________.
,请用你发现的规律,猜想第2018个数为____________.
参考答案:
【答案】![]()
【解析】
首先判断出每个数的正负,然后根据每个数的分子分别是1、3、7、15、…,判断出第n个数的分子是多少;最后根据每个数的分母分别是5、9、17、33、…,判断出第n个数的分母是多少,进而判断出这组数的第n个数是多少,再把n=2018代入,求出第2018个数为多少即可.
解:∵这组数分别是正数、负数、正数、负数、…,
∴这组数的第n个数的正负即(-1)n+1的正负;
∵1=21-1,3=22-1,7=23-1,15=24-1,
∴第n个数的分子是:2n-1;
∵5=4×(21-1-1)+5,9=4×(22-1-1)+5,17=4×(23-1-1)+5,33=4×(24-1-1)+5,
∴第n个数的分母是:4×(2n-1-1)+5=2n+1+1;
∴这组数的第n个数是:
(-1)n+1·![]() ,
,
∴第2018个数为:
(-1)2018+1![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点. (Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.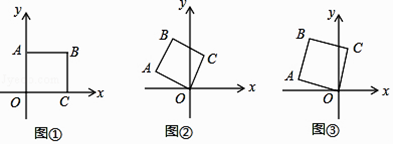
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+2xa+c经过A(﹣4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.

(1)求抛物线的解析式;
(2)点P是第二象限抛物线上的一个动点,连接EP,过点E作EP的垂线l,在l上截取线段EF,使EF=EP,且点F在第一象限,过点F作FM⊥x轴于点M,设点P的横坐标为t,线段FM的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点E作EH⊥ED交MF的延长线于点H,连接DH,点G为DH的中点,当直线PG经过AC的中点Q时,求点F的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,
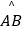 =
= 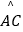 ,∠AOB=40°,则∠ADC的度数是( )
,∠AOB=40°,则∠ADC的度数是( ) 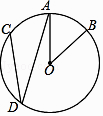
A.15°
B.20°
C.30°
D.40° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×4的正方形方格网中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )
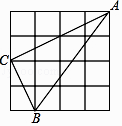
A.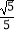
B.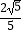
C.
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0
(1)求点C表示的数:
(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动
(i)当P、Q两点在数轴上D点相遇时,求此时C、D两点之间的距离;
(ii),若AP+BQ=2PQ,求时间t.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)分解因式:
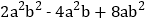 (2)分解因式: 9a2(x—y)+4b2(y—x)
(2)分解因式: 9a2(x—y)+4b2(y—x) (3)分解因式:(x2+y2)2-4x2y2 (4)利用分解因式计算求值:2662-2342
(5)利用分解因式计算求值:已知x-3y=-1,xy=2,求x3y-6x2y2+9xy3的值.
相关试题

