搜索
【题目】如图，在⊙O中， 
= 
，∠AOB=40°，则∠ADC的度数是（ ） 
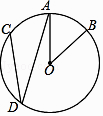
A.15°
B.20°
C.30°
D.40°
参考答案：
【答案】B
【解析】解：连接CO，如图：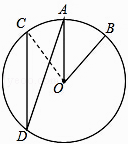 
∵在⊙O中， 
= 
，
∴∠AOC=∠AOB，
∵∠AOB=40°，
∴∠AOC=40°，
∴∠ADC= 
∠AOC=20°，
故选B．
【考点精析】认真审题，首先需要了解圆心角、弧、弦的关系(在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等；在同圆或等圆中，同弧等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半)，还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，C，P是
上两点，AB=13，AC=5． 
（1）如图（1），若点P是 的中点，求PA的长；
（2）如图（2），若点P是
的中点，求PA的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，将边长为2的正方形OABC如图①放置，O为原点． （Ⅰ）若将正方形OABC绕点O逆时针旋转60°时，如图②，求点A的坐标；
（Ⅱ）如图③，若将图①中的正方形OABC绕点O逆时针旋转75°时，求点B的坐标．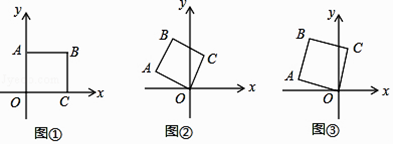
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O为坐标原点，抛物线y=ax2+2xa+c经过A（﹣4，0），B（0，4）两点，与x轴交于另一点C，直线y=x+5与x轴交于点D，与y轴交于点E．
（1）求抛物线的解析式；
（2）点P是第二象限抛物线上的一个动点，连接EP，过点E作EP的垂线l，在l上截取线段EF，使EF=EP，且点F在第一象限，过点F作FM⊥x轴于点M，设点P的横坐标为t，线段FM的长度为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；
（3）在（2）的条件下，过点E作EH⊥ED交MF的延长线于点H，连接DH，点G为DH的中点，当直线PG经过AC的中点Q时，求点F的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如下一组数:
，请用你发现的规律，猜想第2018个数为____________. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在4×4的正方形方格网中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则图中∠ABC的余弦值是（ ）
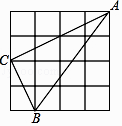
A.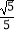
B.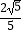
C.
D.2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0
(1)求点C表示的数:
(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动
(i)当P、Q两点在数轴上D点相遇时,求此时C、D两点之间的距离；
(ii),若AP+BQ=2PQ,求时间t.
相关试题
