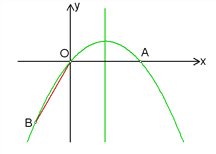
【题目】如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1) ![]() . (2)
. (2) ![]() (3)
(3) ![]()
【解析】【试题分析】(1)在直角三角形BCO中利用三角函数求解;(2)知道抛物线与x轴的两个交点,设成交点式求解;(3)抛物线的对称轴是直线x=2,设点P的坐标为(2, y).
分三种情况讨论:①当OP=OB=4时,OP2=16.所以4+y2=16.解得![]() .
.
②当BP=BO=4时,BP2=16.所以![]() .解得
.解得![]() .
.
③当PB=PO时,PB2=PO2.所以![]() .解得
.解得![]() .故求.
.故求.
【试题解析】
(1)如图1,过点B作BC⊥y轴,垂足为C.
在Rt△OBC中,∠BOC=30°,OB=4,所以BC=2, ![]() .
.
所以点B的坐标为![]() .
.
(2)因为抛物线与x轴交于O、A(4, 0),设抛物线的解析式为y=ax(x-4),
代入点B![]() ,
, ![]() .解得
.解得![]() .
.
所以抛物线的解析式为![]() .
.
(3)抛物线的对称轴是直线x=2,设点P的坐标为(2, y).
①当OP=OB=4时,OP2=16.所以4+y2=16.解得![]() .
.
当P在![]() 时,B、O、P三点共线(如图1).
时,B、O、P三点共线(如图1).
②当BP=BO=4时,BP2=16.所以![]() .解得
.解得![]() .
.
③当PB=PO时,PB2=PO2.所以![]() .解得
.解得![]() .
.
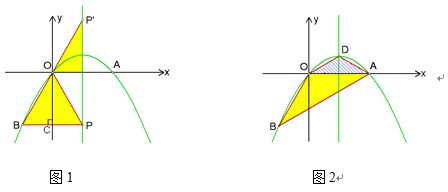
综合①、②、③,点P的坐标为![]() ,如图2所示.
,如图2所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
(1)用“>”“<”或“=”填空:b______0,a+b______0,a-c______0,b-c______0;
(2)|b-1|+|a-1|=________;
(3)化简:|a+b|+|a-c|-|b|+|b-c|.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明将他的7次数学测验成绩按顺序绘成了两幅统计图,依此来观察自己近期数学的学习情况和成绩的进步情况.
(1)甲、乙两幅统计图所表示的数据相同吗?甲图和乙图给人造成的感觉各是什么?
(2)若小明要向他的父母说明他的数学成绩在努力后的情况,他将向父母展示哪幅统计图,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是不为1的有理数,我们把
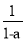 称为a的差倒数,如2的差倒数是
称为a的差倒数,如2的差倒数是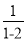 =-1.现已知a1=
=-1.现已知a1=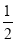 ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数.
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数.(1)求a2,a3,a4的值.
(2)根据(1)的计算结果,请猜想并写出a2018·a2019·a2020的值.
(3)计算:a1+a2+a3+…+a2018+a2019.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图
【1】求这10个样本数据的平均数、众数和中位数;
【2】根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=
 ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.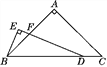
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
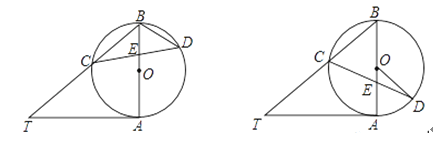
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC,求∠CDO的大小.
相关试题

