【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
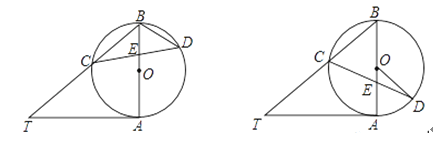
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC,求∠CDO的大小.
参考答案:
【答案】(1)∠T==40°,∠CDB=40°;(2)∠CDO=15°.
【解析】试题分析:(1)根据切线的性质:圆的切线垂直于经过切点的半径,得∠TAB=90°,根据三角形内角和得∠T的度数,由直径所对的圆周角是直角和同弧所对的圆周角相等得∠CDB的度数;
(2)如图②,连接AD,根据等边对等角得:∠BCE=∠BEC=65°,利用同圆的半径相等知:OA=OD,同理∠ODA=∠OAD=65°,由此可得结论.
试题解析:(1)如图,连接AC,
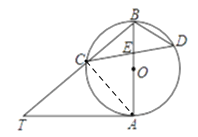
∵AB是⊙O的直径,AD是⊙O的切线,
∴AT⊥AB,即∠TAB=90°
∵∠ABT=50°,
∴∠T=90°-∠ABT=40°
由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90°-∠ABC=40°
∴∠CDB=∠CAB=40°;
(2)如图,连接AD
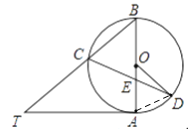
在△BCE中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°
∵OA=OD
∴∠ODA=∠OAD=65°
∵∠ADC=∠ABC=50°
∴∠CDO=∠ODA-∠ADC=15°
-
科目: 来源: 题型:
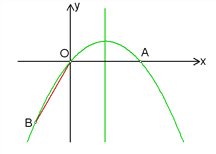
查看答案和解析>>【题目】如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过A、O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图
【1】求这10个样本数据的平均数、众数和中位数;
【2】根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=
 ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.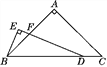
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家使用的是分时电表,按平时段(6:00~22:00)和谷时段(22:00~次日6:00)分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2012年1月至5月的平时段和谷时段的用电量分别用折线图表示(如下图),同时将前4个月的用电量和相应电费制成表格(如下表).
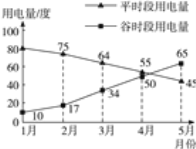
月用电量(度)
电费(元)
1月
90
51.80
2月
92
50.85
3月
98
49.24
4月
105
48.55
5月
根据上述信息,解答下列问题:
(1)计算5月份的用电量和相应电费,将所得结果填入表中;
(2)小明家这5个月的月平均用电量为__________度;
(3)小明家这5个月的月平均用电量呈__________趋势(选择“上升”或“下降”);这5个月每月电费呈__________趋势(选择“上升”或“下降”);
(4)小明预计7月份家中用电量很大,估计7月份用电量可达500度,相应电费将达243元,请你根据小明的估计,计算出7月份小明家平时段用电量和谷时段用电量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用
 纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.
纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.设在同一家复印店一次复印文件的页数为
 (
( 为非负整数).
为非负整数).(1)根据题意,填写下表:
一次复印页数(页)
5
10
20
30
…
甲复印店收费(元)
2
…
乙复印店收费(元)


…
(2)设在甲复印店复印收费
 元,在乙复印店复印收费
元,在乙复印店复印收费 元,分别写出
元,分别写出 关于
关于 的函数关系式;
的函数关系式;(3)当
 时,顾客在哪家复印店复印花费少?请说明理由.
时,顾客在哪家复印店复印花费少?请说明理由.
相关试题

