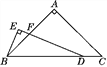
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
参考答案:
【答案】BE=![]() DF
DF
【解析】试题分析:BE与DH的延长线交于G点,由DH∥AC得到∠BDH=45°,则△HBD为等腰直角三角形,于是HB=HD,由∠EBF=22.5°得到DE平分∠BDG,
根据等腰三角形性质得BE=GE,即BE=![]() BG,然后根据“AAS”证明△BGH≌△DFH,则BG=DF,所以BE=
BG,然后根据“AAS”证明△BGH≌△DFH,则BG=DF,所以BE=![]() FD.
FD.
试题解析:
BE=![]() FD.理由:
FD.理由:
BE与DH的延长线交于G点,如图所示:
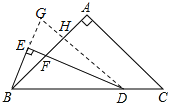
∵DH∥AC,
∴∠BDH=∠C=45°,
∴△HBD为等腰直角三角形
∴HB=HD,
而∠EBF=22.5°,
∵∠EDB=![]() ∠C=22.5°,
∠C=22.5°,
∴DE平分∠BDG,
而DE⊥BG,
∴BE=GE,即BE=![]() BG,
BG,
∵∠DFH+∠FDH=∠G+∠FDH=90°,
∴∠DFH=∠G,
∵∠GBH=90°-∠G,∠FDH=90°-∠G,
∴∠GBH=∠FDH
在△BGH和△DFH中,
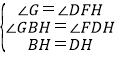
∴△BGH≌△DFH(AAS),
∴BG=DF,
∴BE=![]() FD.
FD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式
(1)6xz﹣9xy
(2)8a3﹣8a2+2a
(3)2ax2﹣18a3
(4)x2﹣4x﹣12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是抛物线y=2(x﹣2)2对称轴上的一个动点,直线x=t平行y轴,分别与y=x、抛物线交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A. aa2=a2B. (a+1)2=a2+1C. x6÷x2=x3D. (-ab)3=-a3b3
-
科目: 来源: 题型:
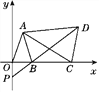
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“两直线平行,同旁内角相等”的逆命题是_______命题 (填“真”或“假”) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( )
A.a=﹣2
B.a=﹣1
C.a=1
D.a=2
相关试题

