【题目】某校为了弘扬中华传统文化,了解学生整体阅读能力,组织全校的1000名学生进行一次阅读理解大赛.从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制了频数分布表和频数分布直方图:
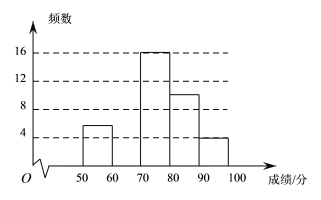
分组/分 | 频数 | 频率 |
50≤x<60 | 6 | 0.12 |
60≤x<70 |
| 0.28 |
70≤x<80 | 16 | 0.32 |
80≤x<90 | 10 | 0.20 |
90≤x≤100 | 4 | 0.08 |
(1)频数分布表中的![]() ;
;
(2)将上面的频数分布直方图补充完整;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,估计该校进入决赛的学生大约有 人.
参考答案:
【答案】(1)14;(2)补图见解析;(3)80.
【解析】
(1)根据第1组频数及其频率求得总人数,总人数乘以第2组频率可得a的值;
(2)把上面的频数分布直方图补充完整;
(3)根据样本中90分及90分以上的百分比,乘以1000即可得到结果.
(1)∵被调查的总人数为6÷0.12=50人,
∴a=50×0.28=14,
故答案为:14;
(2)补全频数分布直方图如下:

(3)估计该校进入决赛的学生大约有1000×0.08=80人,
故答案为:80.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等边
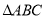 中,
中,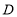 在边
在边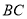 上,
上,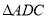 绕顶点
绕顶点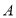 旋转到
旋转到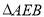 位置,
位置,(1)指出旋转中心,旋转方向,其中一个旋转角及其大小.
(2)指出
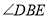 的大小以及联结
的大小以及联结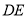 后
后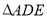 的形状.
的形状.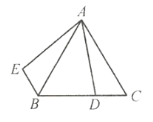
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=ax2+bx+c的图象开口向上,且经过点A(0,
 ).
).(1)若此函数的图象经过点(1,0)、(3,0),求此函数的表达式;
(2)若此函数的图象经过点B(2,﹣
 ),且与x轴交于点C、D.
),且与x轴交于点C、D.①填空:b=_____(用含α的代数式表示);
②当CD2的值最小时,求此函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形
 ,
,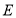 为平面内任意一点,连接
为平面内任意一点,连接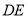 ,将线段
,将线段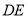 绕点
绕点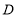 顺时针旋转
顺时针旋转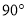 得到
得到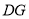 ,当点
,当点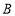 ,
,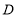 ,
,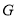 在一条直线时,若
在一条直线时,若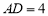 ,
,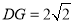 ,则
,则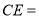 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形
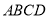 中,长
中,长 ,宽
,宽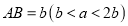 ,四边形
,四边形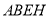 和四边形
和四边形 都是正方形.
都是正方形.(1)求四边形
 的面积(用含
的面积(用含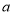 、
、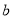 的代数式表示);
的代数式表示);(2)当
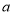 、
、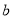 满足什么等量关系时,图形是一个轴对称图形.
满足什么等量关系时,图形是一个轴对称图形.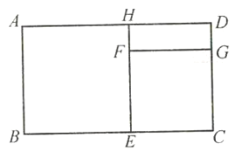
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
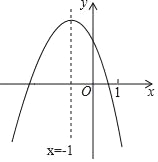
A. 4个 B. 3个 C. 2个 D. 1个
相关试题

