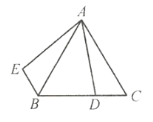
【题目】等边![]() 中,
中,![]() 在边
在边![]() 上,
上,![]() 绕顶点
绕顶点![]() 旋转到
旋转到![]() 位置,
位置,
(1)指出旋转中心,旋转方向,其中一个旋转角及其大小.
(2)指出![]() 的大小以及联结
的大小以及联结![]() 后
后![]() 的形状.
的形状.
参考答案:
【答案】(1)顶点A为旋转中心,旋转方向顺时针,旋转角是![]() 或
或![]() ,旋转角大小为
,旋转角大小为![]() ;(2)
;(2)![]() ,
,![]() 是等边三角形.
是等边三角形.
【解析】
(1)由题意可知,顶点A为旋转中心,旋转后,边AC对应边为AB,边AD对应边为AE,线段CD对应线段为BE,所以![]() 是绕顶点
是绕顶点![]() 顺时针旋转到
顺时针旋转到![]() 位置,旋转角为
位置,旋转角为![]() 或
或![]() ;
;
(2)根据旋转对称图形的性质可知,![]() ,从而可求得
,从而可求得![]() ;同时由旋转对称图形的性质可知AE=AD,又
;同时由旋转对称图形的性质可知AE=AD,又![]() ,即可得
,即可得![]() 的形状.
的形状.
(1)由题意可知,顶点A为旋转中心,![]() 是绕顶点
是绕顶点![]() 顺时针旋转到
顺时针旋转到![]() 位置,
位置,
![]() 旋转角是
旋转角是![]() 或
或![]() ,
,
在等边![]() 中,
中,![]() ,即旋转角大小为
,即旋转角大小为![]() ;
;
(2)根据旋转的性质可知,![]() ,AE=AD,
,AE=AD,
![]() ,
,
又![]() 和
和![]() 同为旋转角,
同为旋转角,
![]() ,
,
在![]() 中
中 ,
,
![]() 是等边三角形.
是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料解决问题
两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,例如37和82,它们各数位上的数字之和分别为3+7和8+2,显然3+7=8+2=10故37和82互为“调和数”.
(1)下列说法错误的是
A.123和51互为调和数” B.345和513互为“调和数
C.2018和8120互为“调和数” D.两位数
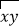 和
和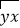 互为“调和数”
互为“调和数”(2)若A、B是两个不等的两位数,A=
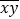 ,B=
,B=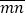 ,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A.
,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】图
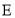 为2002年世界数学家大会的会标,它是用四个形状相同、大小相等的直角三角形拼成的正方形,请通过图形的运动,在右侧网格中补全此会标.
为2002年世界数学家大会的会标,它是用四个形状相同、大小相等的直角三角形拼成的正方形,请通过图形的运动,在右侧网格中补全此会标.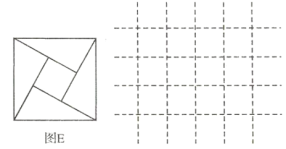
(1)问此正方形会标是旋转对称图形吗?答:______.
(2)若会标中直角三角形的两条直角边长分别为
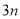 和
和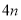 ,请用含
,请用含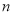 (其中
(其中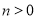 )的代数式表示出此正方形会标的面积.
)的代数式表示出此正方形会标的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=ax2+bx+c的图象开口向上,且经过点A(0,
 ).
).(1)若此函数的图象经过点(1,0)、(3,0),求此函数的表达式;
(2)若此函数的图象经过点B(2,﹣
 ),且与x轴交于点C、D.
),且与x轴交于点C、D.①填空:b=_____(用含α的代数式表示);
②当CD2的值最小时,求此函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了弘扬中华传统文化,了解学生整体阅读能力,组织全校的1000名学生进行一次阅读理解大赛.从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制了频数分布表和频数分布直方图:
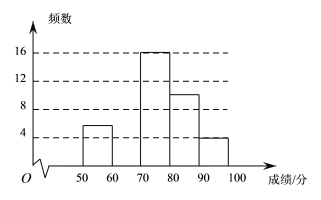
分组/分
频数
频率
50≤x<60
6
0.12
60≤x<70

0.28
70≤x<80
16
0.32
80≤x<90
10
0.20
90≤x≤100
4
0.08
(1)频数分布表中的
 ;
;(2)将上面的频数分布直方图补充完整;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,估计该校进入决赛的学生大约有 人.
相关试题

