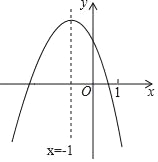
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
参考答案:
【答案】D
【解析】①因为二次函数的对称轴是直线x=﹣1,由图象可得左交点的横坐标大于﹣3,小于﹣2,
所以﹣![]() =﹣1,可得b=2a,
=﹣1,可得b=2a,
当x=﹣3时,y<0,
即9a﹣3b+c<0,
9a﹣6a+c<0,
3a+c<0,
∵a<0,
∴4a+c<0,
所以①选项结论正确;
②∵抛物线的对称轴是直线x=﹣1,
∴y=a﹣b+c的值最大,
即把x=m(m≠﹣1)代入得:y=am2+bm+c<a﹣b+c,
∴am2+bm<a﹣b,
m(am+b)+b<a,
所以此选项结论不正确;
③ax2+(b﹣1)x+c=0,
△=(b﹣1)2﹣4ac,
∵a<0,c>0,
∴ac<0,
∴﹣4ac>0,
∵(b﹣1)2≥0,
∴△>0,
∴关于x的一元二次方程ax2+(b﹣1)x+c=0有实数根;
④由图象得:当x>﹣1时,y随x的增大而减小,
∵当k为常数时,0≤k2≤k2+1,
∴当x=k2的值大于x=k2+1的函数值,
即ak4+bk2+c>a(k2+1)2+b(k2+1)+c,
ak4+bk2>a(k2+1)2+b(k2+1),
所以此选项结论不正确;
所以正确结论的个数是1个,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了弘扬中华传统文化,了解学生整体阅读能力,组织全校的1000名学生进行一次阅读理解大赛.从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制了频数分布表和频数分布直方图:
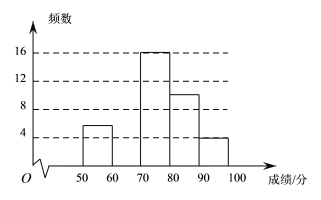
分组/分
频数
频率
50≤x<60
6
0.12
60≤x<70

0.28
70≤x<80
16
0.32
80≤x<90
10
0.20
90≤x≤100
4
0.08
(1)频数分布表中的
 ;
;(2)将上面的频数分布直方图补充完整;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,估计该校进入决赛的学生大约有 人.
-
科目: 来源: 题型:
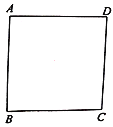
查看答案和解析>>【题目】已知:正方形
 ,
, 为平面内任意一点,连接
为平面内任意一点,连接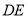 ,将线段
,将线段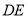 绕点
绕点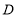 顺时针旋转
顺时针旋转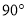 得到
得到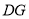 ,当点
,当点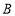 ,
,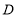 ,
,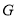 在一条直线时,若
在一条直线时,若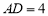 ,
,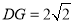 ,则
,则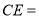 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形
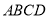 中,长
中,长 ,宽
,宽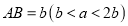 ,四边形
,四边形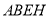 和四边形
和四边形 都是正方形.
都是正方形.(1)求四边形
 的面积(用含
的面积(用含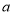 、
、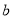 的代数式表示);
的代数式表示);(2)当
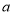 、
、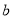 满足什么等量关系时,图形是一个轴对称图形.
满足什么等量关系时,图形是一个轴对称图形.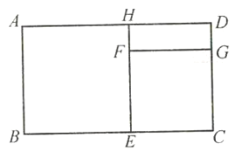
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
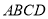 中,
中,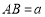 ,
,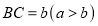 ,将长方形
,将长方形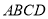 绕点
绕点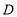 逆时针旋转
逆时针旋转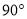 ,点
,点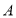 、
、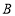 、
、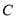 分别对应点
分别对应点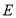 、
、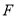 、
、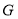 .
.(1)画出长方形
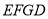 ;
;(2)联结
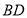 、
、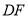 、
、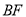 ,请用含有
,请用含有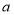 、
、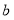 的代数式表示
的代数式表示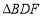 的面积;
的面积;(3)如果
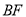 交
交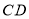 于点
于点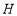 ,请用含有
,请用含有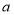 、
、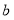 的代数式表示
的代数式表示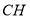 的长度.
的长度.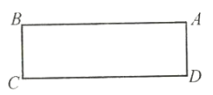
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简、在求值:
(1)(4a2-3a)-(1-4a+4a2),其中a=-2
(2)有8个算式,排成4行2列
2+2,2×2
3+
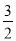 ,3×
,3×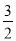
4+
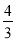 ,4×
,4×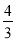
5+
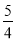 ,5×
,5×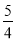
①同一行中两个算式的结果怎样?
②算式2019+
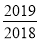 和2019×
和2019×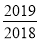 的结果相等吗?
的结果相等吗?③请你写出算式,试一试,再探索其规律,用含自然数n的代数式表示这一规律.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
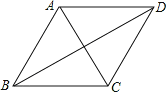
A. △ABD与△ABC的周长相等
B. △ABD与△ABC的面积相等
C. 菱形的周长等于两条对角线之和的两倍
D. 菱形的面积等于两条对角线之积的两倍
相关试题

