【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO,连结CD 
(1)求证:CD是⊙O的切线;
(2)若AB=2,CD= ![]() ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号)
参考答案:
【答案】
(1)证明:连接OD,
∵AD∥OC,
∴∠1=∠3,∠2=∠4
∵OA=OD
∴∠3=∠4
∴∠1=∠2,
在△OCB与△OCD中. 
∴△OCB≌△OCD.(SAS).
∴∠ODC=∠OBC.
∵BC是⊙O的切线
∴∠OBC=90°.
∴∠ODC=90°.
∴OD⊥CD.
∴CD切⊙O于D;
(2)解:由(1)知:CD、BC是⊙O的切线,
∴BC=CD= ![]() ,
,
在Rt△OCB中,
∵OB= ![]() AB=1,
AB=1,
∴OC= ![]() ,
,
由(1)知:∠2=∠4,
∵AB是直径,
∴∠ADB=90°.
∴∠ADB=∠ABC=90°.
∴△OCB∽△ABD,
∴ ![]()
即 ![]() ,
,
∴ ![]() ;
;

【解析】(1)连接OD,SAS证明△ODC≌△OBC,得出∠CDO=∠CBO=90°,即可得出CD是⊙O的切线;(2)先求出OB,OC的长,再运用△ADB∽△OBC,求出AD的长.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,∠ACB的平分线交AB于D,已知∠DCB=2∠B,求∠ACD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,∠ABC=135°,CD=6,AB=2,则四边形ABCD的面积为___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.现将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2018次,点B的落点依次为B1,B2,B3,B4,…,则B2018的坐标为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
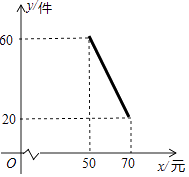
(1)当售价在50~70元时,求每月销售量为y与x的函数关系式?
(2)当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
(3)若该商店每月采购这种新商品的进货款不低于1760元,则该商品每月最大利润为元. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为矩形ABCD中AD边中点,将矩形ABCD沿CE折叠,使点D落在矩形内部的点F处,延长CF交AB于点G,连接AF

(1)求证:AF∥CE;
(2)探究线段AF,EF,EC之间的数量关系,并说明理由;
(3)若BC=6,BG=8,求AF的长. -
科目: 来源: 题型:
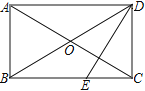
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1) 求证:四边形ABCD是矩形
(2) 若DE⊥AC交BC于E,∠ADB∶∠CDB=2∶3,则∠BDE的度数是多少?
相关试题

