【题目】如图,四边形ABCD中,∠A=∠C=90°,∠ABC=135°,CD=6,AB=2,则四边形ABCD的面积为___________

参考答案:
【答案】16
【解析】
延长AB和DC,两线交于O,求出OB=![]() BC,OD=
BC,OD=![]() OA,OA=AD,BC=OC,设BC=OC=x,则BO=
OA,OA=AD,BC=OC,设BC=OC=x,则BO=![]() x,解直角三角形得出方程,求出x,再分别求出△AOD和△BOC的面积即可.
x,解直角三角形得出方程,求出x,再分别求出△AOD和△BOC的面积即可.
延长AB和DC,两线交于O,
∵∠C=90°,∠ABC=135°,
∴∠OBC=45°,∠BCO=90°,
∴∠O=45°,
∵∠A=90°,
∴∠D=45°,
则OB=![]() BC,OD=
BC,OD=![]() OA,OA=AD,BC=OC,
OA,OA=AD,BC=OC,
设BC=OC=x,则BO=![]() x,
x,
∵CD=6,AB=2,
∴6+x=![]() (
(![]() x+2),
x+2),
解得:x=6-2![]() ,
,
∴OB=6![]() -4,BC=OC=6-2
-4,BC=OC=6-2![]() ,OA=AD=2+6
,OA=AD=2+6![]() -4=6
-4=6![]() -2,
-2,
∴S四边形ABCD=S△OAD-S△OBC
=![]() OAAD-
OAAD-![]() BCOC
BCOC
=![]()
=16,
故答案为:16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲,乙两公司合作,12天可以完成;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,要使乙公司的总施工费较少,则甲公司每天的施工费应低于多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图①,若AB∥CD,点P在AB,CD外部,则有 ∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,∠ACB的平分线交AB于D,已知∠DCB=2∠B,求∠ACD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.现将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2018次,点B的落点依次为B1,B2,B3,B4,…,则B2018的坐标为________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO,连结CD

(1)求证:CD是⊙O的切线;
(2)若AB=2,CD= ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
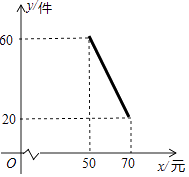
(1)当售价在50~70元时,求每月销售量为y与x的函数关系式?
(2)当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
(3)若该商店每月采购这种新商品的进货款不低于1760元,则该商品每月最大利润为元.
相关试题

