【题目】小颖在一张纸上画一条数轴,并在数轴上标出![]() 、
、![]() 、
、![]() 三个点,点
三个点,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 在原点的右边且与点
在原点的右边且与点![]() 相距
相距![]() 个单位长度.
个单位长度.
(![]() )点
)点![]() 表示的数是__________.
表示的数是__________.
(![]() )将这张纸对折,此时点
)将这张纸对折,此时点![]() 与表示
与表示![]() 的点刚好重合,折痕与数轴交于点
的点刚好重合,折痕与数轴交于点![]() ,求点
,求点![]() 表示的数.
表示的数.
(![]() )若点
)若点![]() 到点
到点![]() 和点
和点![]() 的距离之和为
的距离之和为![]() ,求点
,求点![]() 所表示的数.
所表示的数.
(![]() )点
)点![]() 和点
和点![]() 同时从初始位置沿数轴向左运动,它们的速度分别是每秒
同时从初始位置沿数轴向左运动,它们的速度分别是每秒![]() 个单位长度和每秒
个单位长度和每秒![]() 个单位长度,运动时间是
个单位长度,运动时间是![]() 秒.是否存在
秒.是否存在![]() 的值,使
的值,使![]() 秒后点
秒后点![]() 到原点的距离与点
到原点的距离与点![]() 到原点的距离相等?若存在,请求出
到原点的距离相等?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)12;(2)4;(3)-10.5或14.5;(4)t=![]() 或20s
或20s
【解析】
(1)根据数轴上两点间的距离公式,可求出点B表示的数;
(2)根据对称可知点C到-4和12的距离相等,可求点C表示的数为:(-4+12)÷2=4;
(3)分两种情况讨论:①当![]() 点在A点的左边,②当
点在A点的左边,②当![]() 点在B点的右边,然后利用数轴上两点间的距离公式即可解答;
点在B点的右边,然后利用数轴上两点间的距离公式即可解答;
(4)由t秒后点B到原点的距离是点A到原点距离相等,列出一元一次方程即可.
解:(1)-8+20=12,所以点B表示的数为:12;
(2)(-4+12)÷2=4,
则折痕与数轴有一个交点C表示的数为:4;
(3)∵AB=20,点![]() 到点A和点B的距离之和为25,
到点A和点B的距离之和为25,
∴点![]() 应在线段AB的外,
应在线段AB的外,
分两种情况:
①当![]() 点在A点的左边,设
点在A点的左边,设![]() 点表示数为x,
点表示数为x,
∵|![]() A|=|x-(-8)|=-x-8,
A|=|x-(-8)|=-x-8,
|DB|=|x-12|=12-x,
∴(-x-8)+(12-x)=25,
解得:x=-10.5,
所以此时![]() 点所表示的数为:-10.5,
点所表示的数为:-10.5,
②当![]() 点在B点的右边,设
点在B点的右边,设![]() 点表示数为x,
点表示数为x,
∵|![]() A|=|x-(-8)|=x+8,
A|=|x-(-8)|=x+8,
|![]() B|=|x-12|=x-12,
B|=|x-12|=x-12,
∴(x+8)+(x-12)=25,
解得:x=14.5,
所以此时![]() 点所表示的数为:14.5,
点所表示的数为:14.5,
故若点![]() 到点A和点B的距离之和为25,则点E所表示的数为:-10.5或14.5;
到点A和点B的距离之和为25,则点E所表示的数为:-10.5或14.5;
(4)存在.
由题意得:|-8-t|=|12-2t|
解之得:8+t=12-2t或8+t=2t-12
即t=![]() 或t=20
或t=20
故存在;t的值是![]() 或20.
或20.
所以当t=![]() 或4s时,点B到原点的距离是点A到原点距离相等.
或4s时,点B到原点的距离是点A到原点距离相等.
故答案为:(1)12;(2)4;(3)-10.5或14.5;(4)t=![]() 或20s
或20s
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中(请补画出必要的图形),O为坐标原点,直线y= -2x+4与x、y轴分别交于A、B两点,过线段OA的中点C作x轴的垂线l,分别与直线AB交于点D,与直线y=x+n交于点P。
(1)直接写出点A、B、C、D的坐标:A( ),B( ),C( ),D( )
(2)若△APD的面积等于1,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】彩虹服装店用
 元购进
元购进 件衬衣,很快全部售完.服装店老板以每件
件衬衣,很快全部售完.服装店老板以每件 元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:
元的价格为标准,将超出的记为正数,不足的记为负数,记录如下: ,
, ,
, ,
, ,
, ,
, ,
, ,
, (单位:元).他卖完这
(单位:元).他卖完这 件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】某天下午,出租车司机小李始终在一条南北方向的商业大道上运营,如果规定向北为正方向,他记录的出租车行车里程如下(单位:千米):
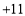 ,
,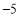 ,
,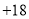 ,
, ,
, ,
,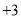 ,
,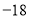 ,
,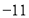
(
 )将最后一名乘客送到目的地时,小李在出车地点的什么方向?距离是多少?
)将最后一名乘客送到目的地时,小李在出车地点的什么方向?距离是多少?(
 )若出租车每千米耗油量为
)若出租车每千米耗油量为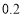 升,那么这天下午小李的出租车共耗油多少升?
升,那么这天下午小李的出租车共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】《算经十书》是指汉、唐一千多年间的十部著名的数学著作,十部书的名称是:《周髀算经》、《九章算术》、《海岛算经》、《张丘建算经》、《夏侯阳算经》、《五经算术》、《缉古算经》、《缀术》、《五曹算经》、《孙子算经》.其中在《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五,屈绳量之,不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条,绳子剩余
 尺;将绳子对折再量木条,木条剩余
尺;将绳子对折再量木条,木条剩余 尺,问绳子、木条长多少尺?”,设绳子长为
尺,问绳子、木条长多少尺?”,设绳子长为 尺,木条长为
尺,木条长为 尺,根据题意,所列方程组正确的是( )
尺,根据题意,所列方程组正确的是( )A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的点E处,折痕为PQ.过点E作EF∥AB交PQ于点F,连接BF

(1)若AP: BP=1:2,则AE的长为 .
(2)求证:四边形BFEP为菱形;
(3)当点E在AD边上移动时,折痕的端点P、Q也随之移动.若限定点P,Q分别在边AB、BC上移动,求出点E在边AD上移动的最大距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B在反比例函数
 (x>0)的图象上,它们的横坐标分别为m,n,且m≠n,过点A,点B都向x轴,y轴作垂线段,其中两条垂线段的交点为C.
(x>0)的图象上,它们的横坐标分别为m,n,且m≠n,过点A,点B都向x轴,y轴作垂线段,其中两条垂线段的交点为C.
(1)如图,当m=2,n=6时,直接写出点C的坐标:
(2)若A(m,n),B(n,m).连接OA、OB、AB,求△AOB的面积:(用含m的代数式表示)
(3)设AD⊥y轴于点D,BE⊥x轴于点E.若
 ,且
,且 ,则当点C在直线DE上时,求p的取值范围.
,则当点C在直线DE上时,求p的取值范围.
相关试题

