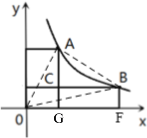
【题目】已知点A,B在反比例函数![]() (x>0)的图象上,它们的横坐标分别为m,n,且m≠n,过点A,点B都向x轴,y轴作垂线段,其中两条垂线段的交点为C.
(x>0)的图象上,它们的横坐标分别为m,n,且m≠n,过点A,点B都向x轴,y轴作垂线段,其中两条垂线段的交点为C.

(1)如图,当m=2,n=6时,直接写出点C的坐标:
(2)若A(m,n),B(n,m).连接OA、OB、AB,求△AOB的面积:(用含m的代数式表示)
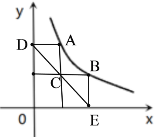
(3)设AD⊥y轴于点D,BE⊥x轴于点E.若![]() ,且
,且![]() ,则当点C在直线DE上时,求p的取值范围.
,则当点C在直线DE上时,求p的取值范围.
参考答案:
【答案】(1)点C坐标为(2,1);(2)S△AOB=![]() (0<m<
(0<m<![]() );(3)
);(3)![]() ≤p≤
≤p≤![]() .
.
【解析】
(1)把n=6代入反比例函数解析式可求出点B坐标,即可得答案;
(2)如图,由反比例函数k的几何意义可得S△AOG=S△BOF,进而可得S△AOB=S四边形AGFB,利用梯形面积公式即可得答案;
(3)如图,由A、B坐标可用m、n表示出点C、E、D坐标,利用待定系数法可得出DE解析式,把C点坐标代入可得m与n的关系,代入![]() 可用n表示出p,根据n的取值范围,利用不等式的性质即可得答案.
可用n表示出p,根据n的取值范围,利用不等式的性质即可得答案.
(1)∵n=6,点B在![]() (x>0)的图象上,它的横坐标分别为n,
(x>0)的图象上,它的横坐标分别为n,
∴y=![]() =1,
=1,
∴B(6,1),
∵m=2,两条垂线段的交点为C,
∴点C坐标为(2,1).
(2)如图,
∵点A,B在反比例函数![]() (x>0)的图象上,
(x>0)的图象上,
∴S△AOG=S△BOF=![]() ×6=3,
×6=3,
∴S△AOB=S△AOG+S四边形AGFB-S△BOF=S四边形AGFB,
∵A(m,n),B(n,m),
∴AG=n,OG=m,OF=n,BF=m,n=![]() ,
,
∵点B在点A右侧,m≠n,m>0,n>0,
∴0<m<![]() ,
,
∴S△AOB=![]() (m+n)(n-m)=
(m+n)(n-m)=![]() (n2-m2)=
(n2-m2)=![]() (0<m<
(0<m<![]() ).
).
(3)如图,
∵点A、B在![]() (x>0)的图象上,它们的横坐标分别为m、n,
(x>0)的图象上,它们的横坐标分别为m、n,
∴A(m,![]() ),B(n,
),B(n,![]() )(m>0,n>0),
)(m>0,n>0),
∴C(m,![]() ),E(n,0),D(0,
),E(n,0),D(0,![]() ),
),
设直线DE的解析式为y=kx+b,
∴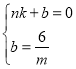 ,
,
解得: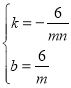 ,
,
∴直线DE的解析式为y=![]() ,
,
∵点C在直线DE上,
∴![]() ,
,
整理得:m=![]() n,
n,
∴![]() =1-
=1-![]() ,
,
∵![]() ,
,
∴2≤2n≤8,
∴![]() ≤
≤![]() ≤
≤![]() ,
,
∴![]() ≤1-
≤1-![]() ≤
≤![]() ,
,
∴p的取值范围为![]() ≤p≤
≤p≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖在一张纸上画一条数轴,并在数轴上标出
 、
、 、
、 三个点,点
三个点,点 表示的数是
表示的数是 ,点
,点 在原点的右边且与点
在原点的右边且与点 相距
相距 个单位长度.
个单位长度.(
 )点
)点 表示的数是__________.
表示的数是__________.(
 )将这张纸对折,此时点
)将这张纸对折,此时点 与表示
与表示 的点刚好重合,折痕与数轴交于点
的点刚好重合,折痕与数轴交于点 ,求点
,求点 表示的数.
表示的数.(
 )若点
)若点 到点
到点 和点
和点 的距离之和为
的距离之和为 ,求点
,求点 所表示的数.
所表示的数.(
 )点
)点 和点
和点 同时从初始位置沿数轴向左运动,它们的速度分别是每秒
同时从初始位置沿数轴向左运动,它们的速度分别是每秒 个单位长度和每秒
个单位长度和每秒 个单位长度,运动时间是
个单位长度,运动时间是 秒.是否存在
秒.是否存在 的值,使
的值,使 秒后点
秒后点 到原点的距离与点
到原点的距离与点 到原点的距离相等?若存在,请求出
到原点的距离相等?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】《算经十书》是指汉、唐一千多年间的十部著名的数学著作,十部书的名称是:《周髀算经》、《九章算术》、《海岛算经》、《张丘建算经》、《夏侯阳算经》、《五经算术》、《缉古算经》、《缀术》、《五曹算经》、《孙子算经》.其中在《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五,屈绳量之,不足一尺,问木长几何?”大致意思是:“用一根绳子去量一根木条,绳子剩余
 尺;将绳子对折再量木条,木条剩余
尺;将绳子对折再量木条,木条剩余 尺,问绳子、木条长多少尺?”,设绳子长为
尺,问绳子、木条长多少尺?”,设绳子长为 尺,木条长为
尺,木条长为 尺,根据题意,所列方程组正确的是( )
尺,根据题意,所列方程组正确的是( )A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的点E处,折痕为PQ.过点E作EF∥AB交PQ于点F,连接BF

(1)若AP: BP=1:2,则AE的长为 .
(2)求证:四边形BFEP为菱形;
(3)当点E在AD边上移动时,折痕的端点P、Q也随之移动.若限定点P,Q分别在边AB、BC上移动,求出点E在边AD上移动的最大距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的统计图反映了我国2013年到2017年国内生产总值情况.(以上数据摘自国家统计局《中华人民共和国2017年国民经济和社会发展统计公报》,其中国内生产总值绝对数按现价计算,增长速度按不变价格计算)

根据统计图提供的信息,下列推断合理的是
A.从2013-2017年,我国国内生产总值逐年下降
B.从2013-2017年,我国国内生产总值的增长率逐年下降
C.从2013-2017年,我国国内生产总值的平均增长率约为6.7%
D.计算同上年相比的增量,2017年我国国内生产总值的增量为近几年最多
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=24,BC=26,CA=14.顺次连接△ABC各边中点,得到△A1B1C1;再顺次连接△A1B1C1各边中点,得到△A2B2C2…如此进行下去,得到
 ,则△A8B8C8的周长为( )
,则△A8B8C8的周长为( )
A.1B.
 C.
C.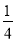 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P在等边△ABC内且∠APC=120°,则
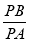 的最小值是( )
的最小值是( )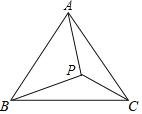
A.
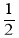 B.
B.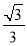 C.
C.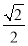 D.
D.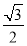
相关试题

