【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交切线AC于点C,OC与圆O交于点E,连结BE、DE.
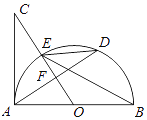
(1)若圆的半径是3,∠EBA是30度,求AD的长度.
(2)求证:∠BED=∠C.
(3)若OA=5,AD=8,求切线AC的长.
参考答案:
【答案】(1)AD=3![]() ;(2)证明见解析;(3)AC=
;(2)证明见解析;(3)AC=![]()
【解析】试题分析:(1)由垂径定理可得AF=DF,要求AD的长度,即要求AF的长度,由∠EBA=30°可以得出∠FOA=60°,进而得出∠FAO=30°,已知OA的长度结合30°余弦值,不难求出AF的长度,即可求出AD的长度;(2)要证∠BED=∠C即要证明∠DAB=∠C,由于∠C+∠CAF=90°,∠DAB+∠CAF=90°,不难证明;(3)连接BD,BD⊥AD,由勾股定理求出BD的长度,再由△OAC∽△BDA写出对应边的比值,即可求出AC的长度.
试题解析:
(1)解:∵∠EBA=30°,
∴∠AOF=60°,
∵OC⊥AD,
∴∠OAF=30°,AD=2AF,
∵AO=3,
∴AF=AO·cos30°=3×![]() =
=![]() ,
,
∴AD=2AF=3![]() ;
;
(2)
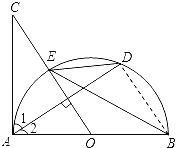
∵AC是⊙O的切线,AB是⊙O直径,
∴AB⊥AC.
∴∠1+∠2=90°,
∵OC⊥AD,
∴∠1+∠C=90°,
∴∠C=∠2,
∵∠BED=∠2,
∴∠BED=∠C;
(3)解:连接BD,
∵AB是⊙O直径,
∴∠ADB=90°,
∴BD=![]() =6,
=6,
∴△OAC∽△BDA,
∴OA∶BD=AC∶DA,
即5:6=AC:8,
∴AC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 为坐标原点,矩形
为坐标原点,矩形 的顶点
的顶点 、
、 ,将矩形
,将矩形 的一个角沿直线
的一个角沿直线 折叠,使得点
折叠,使得点 落在对角线
落在对角线 上的点
上的点 处,折痕与
处,折痕与 轴交于点
轴交于点 .
.(1)求线段
 的长度;
的长度;(2)求直线
 所对应的函数表达式;
所对应的函数表达式;(3)若点
 在线段
在线段 上,在线段
上,在线段 上是否存在点
上是否存在点 ,使以
,使以 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期
一
二
三
四
五
六
日
增减/吨
﹣1
+3
﹣2
+4
+7
﹣5
﹣10
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队承担了100米的道路改造工程任务,在确保工程质量的前提下,实际施工时每天改造道路比原计划多10米,结果提前5天完成了任务,求原计划平均每天改造道路多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别
次数x
频数(人数)
第1组
80≤x<100
6
第2组
100≤x<120
8
第3组
120≤x<140
a
第4组
140≤x<160
18
第5组
160≤x<180
6

请结合图表完成下列问题:
(1)表中的a=________;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第________组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120为不合格;120≤x<140,为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或九年级同学提一条合理化建议:_________________________________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)探究发现
数学活动课上,小明说“若直线
 向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”
向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”经过一番讨论,小组成员展示了他们的解答过程:
在直线
 上任取点
上任取点 ,
,向左平移3个单位得到点

设向左平移3个单位后所得直线所对应的函数表达式为
 .
.因为
 过点
过点 ,
,所以
 ,
,所以
 ,
,填空:所以平移后所得直线所对应函数表达式为
(2)类比运用
已知直线
 ,求它关于
,求它关于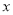 轴对称的直线所对应的函数表达式;
轴对称的直线所对应的函数表达式;(3)拓展运用
将直线
 绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .
绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 . -
科目: 来源: 题型:
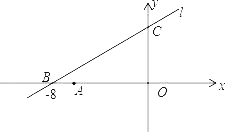
查看答案和解析>>【题目】如图直线l:y=kx+6与x轴、y轴分别交于点B、C两点,点B的坐标是(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值.
(2)若点P是直线l在第二象限内一个动点,当点P运动到什么位置时,△PAC的面积为3,求出此时直线AP的解析式.
(3)在x轴上是否存在一点M,使得△BCM为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
相关试题

