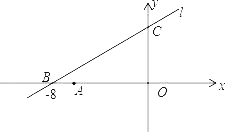
【题目】如图直线l:y=kx+6与x轴、y轴分别交于点B、C两点,点B的坐标是(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值.
(2)若点P是直线l在第二象限内一个动点,当点P运动到什么位置时,△PAC的面积为3,求出此时直线AP的解析式.
(3)在x轴上是否存在一点M,使得△BCM为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ,(2)P(﹣4,3);y=
,(2)P(﹣4,3);y=![]() x+9.(3)(﹣18,0),(﹣
x+9.(3)(﹣18,0),(﹣![]() ,0),(2,0)或(8,0),见解析.
,0),(2,0)或(8,0),见解析.
【解析】
(1)由点B的坐标,利用一次函数图象上点的坐标特征可求出k值;
(2)利用一次函数图象上点的坐标特征求出点C的坐标,设点P的坐标为(x,![]() x+6),由S△PAC=S△BOC﹣S△BAP﹣S△AOC结合△PAC的面积为3,可得出关于x的一元一次方程,解之即可得出点P的坐标,再利用待定系数法即可求出此时直线AP的解析式;
x+6),由S△PAC=S△BOC﹣S△BAP﹣S△AOC结合△PAC的面积为3,可得出关于x的一元一次方程,解之即可得出点P的坐标,再利用待定系数法即可求出此时直线AP的解析式;
(3)利用勾股定理求出BC的长度,分CB=CM,BC=BM,MB=MC三种情况考虑:①当CB=CM时,由OM1=OB=8可得出点M1的坐标;②当BC=BM时,由BM2=BM3=BC=10结合点B的坐标可得出点M2,M3的坐标;③当MB=MC时,设OM=t,则M4B=M4C=8﹣t,利用勾股定理可得出关于t的一元一次方程,解之即可得出点M4的坐标.综上,此题得解.
(1)∵直线l:y=kx+6过点B(﹣8,0),
∴0=﹣8k+6,
∴k=![]() .
.
(2)当x=0时,y=![]() x+6=6,
x+6=6,
∴点C的坐标为(0,6).
依照题意画出图形,如图1所示,
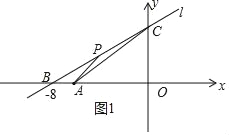
设点P的坐标为(x,![]() x+6),
x+6),
∴S△PAC=S△BOC﹣S△BAP﹣S△AOC,
=![]() ×8×6﹣
×8×6﹣![]() ×2(
×2(![]() x+6)﹣
x+6)﹣![]() ×6×6,
×6×6,
=﹣![]() x=3,
x=3,
∴x=﹣4,
∴点P的坐标为(﹣4,3).
设此时直线AP的解析式为y=ax+b(a≠0),
将A(﹣6,0),P(﹣4,3)代入y=ax+b,
得:![]() ,解得:
,解得: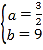 ,
,
∴当点P的坐标为(﹣4,3)时,△PAC的面积为3,此时直线AP的解析式为y=![]() x+9.
x+9.
(3)在Rt△BOC中,OB=8,OC=6,
∴BC=![]() =10.
=10.
分三种情况考虑(如图2所示):
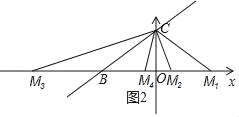
①当CB=CM时,OM1=OB=8,
∴点M1的坐标为(8,0);
②当BC=BM时,BM2=BM3=BC=10,
∵点B的坐标为(﹣8,0),
∴点M2的坐标为(2,0),点M3的坐标为(﹣18,0);
③当MB=MC时,设OM=t,则M4B=M4C=8﹣t,
∴CM42=OM42+OC2,即(8﹣t)2=t2+62,
解得:t=![]() ,
,
∴点M4的坐标为(﹣![]() ,0).
,0).
综上所述:在x轴上存在一点M,使得△BCM为等腰三角形,点M的坐标为(﹣18,0),(﹣![]() ,0),(2,0)或(8,0).
,0),(2,0)或(8,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交切线AC于点C,OC与圆O交于点E,连结BE、DE.
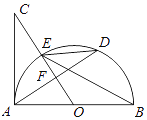
(1)若圆的半径是3,∠EBA是30度,求AD的长度.
(2)求证:∠BED=∠C.
(3)若OA=5,AD=8,求切线AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别
次数x
频数(人数)
第1组
80≤x<100
6
第2组
100≤x<120
8
第3组
120≤x<140
a
第4组
140≤x<160
18
第5组
160≤x<180
6

请结合图表完成下列问题:
(1)表中的a=________;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第________组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120为不合格;120≤x<140,为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或九年级同学提一条合理化建议:_________________________________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)探究发现
数学活动课上,小明说“若直线
 向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”
向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”经过一番讨论,小组成员展示了他们的解答过程:
在直线
 上任取点
上任取点 ,
,向左平移3个单位得到点

设向左平移3个单位后所得直线所对应的函数表达式为
 .
.因为
 过点
过点 ,
,所以
 ,
,所以
 ,
,填空:所以平移后所得直线所对应函数表达式为
(2)类比运用
已知直线
 ,求它关于
,求它关于 轴对称的直线所对应的函数表达式;
轴对称的直线所对应的函数表达式;(3)拓展运用
将直线
 绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .
绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 . -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC 中,AB=15,AC=13,高 AD=12,则△ABC 的周长是( )
A. 42B. 32C. 42 或 32D. 42 或 37
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
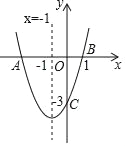
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.
 B.
B.  C.
C.  D.
D. 
相关试题

