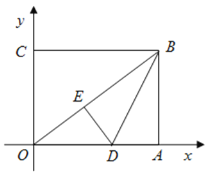
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角沿直线
的一个角沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
(1)求线段![]() 的长度;
的长度;
(2)求直线![]() 所对应的函数表达式;
所对应的函数表达式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)15;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据勾股定理即可解决问题;
(2)设AD=x,则OD=OA=AD=12-x,根据轴对称的性质,DE=x,BE=AB=9,又OB=15,可得OE=OB-BE=15-9=6,在Rt△OED中,根据OE2+DE2=OD2,构建方程即可解决问题;
(3)过点E作EP∥BD交BC于点P,过点P作PQ∥DE交BD于点Q,则四边形DEPQ是平行四边形,再过点E作EF⊥OD于点F,想办法求出最小PE的解析式即可解决问题.
解:(1)由题知:![]() .
.
(2)设![]() ,则
,则![]() ,
,
根据轴对称的性质,![]() ,
,![]() ,
,
又![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得 ![]() ,
,
∴![]() ,
,
∴点![]() ,
,
设直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]() ,
,
则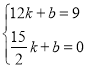 , 解得
, 解得![]() ,
,
∴直线![]() 所对应的函数表达式为:
所对应的函数表达式为:![]() ,
,
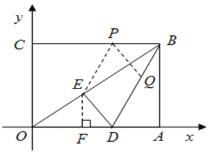
(3)存在,过点![]() 作EP∥DB交
作EP∥DB交![]() 于点
于点![]() ,过点
,过点![]() 作PQ∥ED交
作PQ∥ED交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是平行四边形.再过点
是平行四边形.再过点![]() 作
作![]() 于点
于点![]() ,
,
由![]() ,
,
得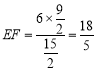 ,即点
,即点![]() 的纵坐标为
的纵坐标为![]() ,
,
又点![]() 在直线
在直线![]() :
:![]() 上,
上,
∴![]() , 解得
, 解得 ![]() , ∴
, ∴![]()
由于EP∥DB,所以可设直线![]() :
:![]() ,
,
∵![]() 在直线
在直线![]() 上
上
∴![]() , 解得
, 解得 ![]() ,
,
∴直线![]() :
:![]() ,
,
令![]() ,则
,则![]() ,
,
解得![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某保温杯专卖店通过市场调研,准备销售
 、
、 两种型号的保温杯,其中每件
两种型号的保温杯,其中每件 种保温杯的进价比
种保温杯的进价比 种保温杯的进价高20元,已知专卖店用3200元购进
种保温杯的进价高20元,已知专卖店用3200元购进 种保温杯的数量与用2560元购进
种保温杯的数量与用2560元购进 种保温杯的数量相同.
种保温杯的数量相同.(1)求两种保温杯的进价;
(2)若
 种保温杯的售价为250元,
种保温杯的售价为250元, 种保温杯的售价为180元,专卖店共进两种保温杯200个,设
种保温杯的售价为180元,专卖店共进两种保温杯200个,设 种保温杯进货
种保温杯进货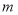 个,求该专卖店获得的总利润
个,求该专卖店获得的总利润 (元)与
(元)与 种保温杯进货数
种保温杯进货数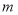 (个)之间的函数关系式,并写出自变量的取值范围.
(个)之间的函数关系式,并写出自变量的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)如图,平行四边形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,点P从O沿OB边向点B移动,点Q从点B沿BC边向点C移动,P,Q同时出发,速度都是1cm/s.
(1)求经过O,B,D三点的抛物线的解析式;
(2)判断P,Q移动几秒时,△PBQ为等腰三角形;
(3)若允许P点越过B点在BC上运动,Q点越过C点在CD上运动,设线PQ与OB,BC,DC围成的图形面积为y(cm2),点P,Q的移动时间为t(s),请写出y与t之间的函数关系式,并写出t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤
 .当∠EPF在△ABC内绕顶点P旋转时(点E不与点A、B重合),上述结论中始终正确的序号有 .
.当∠EPF在△ABC内绕顶点P旋转时(点E不与点A、B重合),上述结论中始终正确的序号有 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期
一
二
三
四
五
六
日
增减/吨
﹣1
+3
﹣2
+4
+7
﹣5
﹣10
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队承担了100米的道路改造工程任务,在确保工程质量的前提下,实际施工时每天改造道路比原计划多10米,结果提前5天完成了任务,求原计划平均每天改造道路多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交切线AC于点C,OC与圆O交于点E,连结BE、DE.
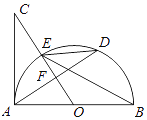
(1)若圆的半径是3,∠EBA是30度,求AD的长度.
(2)求证:∠BED=∠C.
(3)若OA=5,AD=8,求切线AC的长.
相关试题

