【题目】如图一,点![]() 在线段
在线段![]() 上,图中有三条线段
上,图中有三条线段![]() 、
、![]() 和
和![]() ,若其中一条线段的长度是另外一条线段长度的
,若其中一条线段的长度是另外一条线段长度的![]() 倍,则称点
倍,则称点![]() 是线段
是线段![]() 的“巧点”.
的“巧点”.
(1)填空:线段的中点 这条线段的巧点(填“是”或“不是”或“不确定是”)
(问题解决)
(2)如图二,点![]() 和
和![]() 在数轴上表示的数分别是
在数轴上表示的数分别是![]() 和
和![]() ,点
,点![]() 是线段
是线段![]() 的巧点,求点
的巧点,求点![]() 在数轴上表示的数。
在数轴上表示的数。
(应用拓展)
(3)在(2)的条件下,动点![]() 从点
从点![]() 处,以每秒
处,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 向点
向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 向点
向点![]() 匀速运动,当其中一点到达中点时,两个点运动同时停止,当
匀速运动,当其中一点到达中点时,两个点运动同时停止,当![]()
![]() 、
、![]() 三点中,其中一点恰好是另外两点为端点的线段的巧点时,直接写出运动时间
三点中,其中一点恰好是另外两点为端点的线段的巧点时,直接写出运动时间![]() 的所有可能值.
的所有可能值.

参考答案:
【答案】(1)是;(2)10或0或20;(3) ![]() ;t=6;
;t=6;![]() ;t=12;
;t=12;![]() ;
;![]() .
.
【解析】
(1)根据新定义,结合中点把原线段分成两短段,满足原线段是短线段的2倍关系,进行判断即可;
(2)由题意设C点表示的数为x,再根据新定义列出合适的方程即可;
(3)根据题意先用t的代数式表示出线段AP,AQ,PQ,再根据新定义列出方程,得出合适的解即可求出t的值.
解:(1)因原线段是中点分成的短线段的2倍,所以线段的中点是这条线段的巧点,
故答案为:是;
(2)设C点表示的数为x,则AC=x+20,BC=40-x,AB=40+20=60,
根据“巧点”的定义可知:
①当AB=2AC时,有60=2(x+20),
解得,x=10;
②当BC=2AC时,有40-x=2(x+20),
解得,x=0;
③当AC=2BC时,有x+20=2(40-x),
解得,x=20.
综上,C点表示的数为10或0或20;
(3)由题意得 ,
,
(i)、若0≤t≤10时,点P为AQ的“巧点”,有
①当AQ=2AP时,60-4t=2×2t,
解得,![]() ,
,
②当PQ=2AP时,60-6t=2×2t,
解得,t=6;
③当AP=2PQ时,2t=2(60-6t),
解得,![]() ;
;
综上,运动时间![]() 的所有可能值有
的所有可能值有![]() ;t=6;
;t=6;![]() ;
;
(ii)、若10<t≤15时,点Q为AP的“巧点”,有
①当AP=2AQ时,2t=2×(60-4t),
解得,t=12;
②当PQ=2AQ时,6t-60=2×(60-4t),
解得,![]() ;
;
③当AQ=2PQ时,60-4t=2(6t-60),
解得,![]() .
.
综上,运动时间![]() 的所有可能值有:t=12;
的所有可能值有:t=12;![]() ;
;![]() .
.
故,运动时间![]() 的所有可能值有:
的所有可能值有:![]() ;t=6;
;t=6;![]() ;t=12;
;t=12;![]() ;
;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),
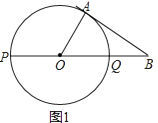
(1)当线段AB所在的直线与圆O相切时,求弧AQ的长(图1);
(2)若∠AOB=120°,求AB的长(图2);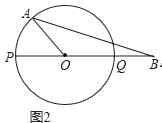
(3)如果线段AB与圆O有两个公共点A、M,当AO⊥PM于点N时,求tan∠MPQ的值(图3).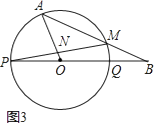
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等腰
 中,
中, ,
, 为
为 中点,连接
中点,连接 ,
,
(1)求证:
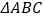 是等边三角形
是等边三角形(2)如图2,在
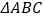 内有一点
内有一点 ,连接
,连接 、
、 、
、 ,若
,若 ,求
,求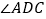 的度数
的度数(3)如图3,在(2)的条件下,在
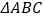 外有一点
外有一点 ,连接
,连接 、
、 、若
、若 ,
, ,
, ,求线段
,求线段 的长.
的长.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,ABCD的顶点的坐标分别为A(﹣6,9),B(0,9),C(3,0),D(﹣3,0),抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)过A、B两点,顶点为M.

(1)若抛物线过点C,求抛物线的解析式;
(2)若抛物线的顶点M落在△ACD的内部(包括边界),求a的取值范围;
(3)若a<0,连结CM交线段AB于点Q(Q不与点B重合),连接DM交线段AB于点P,设S1=S△ADP+S△CBQ , S2=S△MPQ , 试判断S1与S2的大小关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
 的边长为
的边长为  ,
,  ,弧
,弧  是以点
是以点  为圆心、
为圆心、  长为半径的弧,弧
长为半径的弧,弧  是以点
是以点  为圆心、
为圆心、  长为半径的弧,则阴影部分的面积为( )
长为半径的弧,则阴影部分的面积为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点
 在
在 轴正半轴,点
轴正半轴,点 在
在 轴负半轴,连接
轴负半轴,连接 ,
, ,
,
(1)求点
 坐标
坐标(2)如图2,点
 是线段
是线段 上一点,连接
上一点,连接 ,以
,以 为直角边做等腰直角
为直角边做等腰直角 ,
, ,设点
,设点 的横坐标为
的横坐标为 ,求点
,求点 的坐标(用含
的坐标(用含 的代数式表示)
的代数式表示)(3)在(2)的条件下,如图3,在
 延长线上有一点
延长线上有一点 ,过点
,过点 作
作 的平行线,交
的平行线,交 轴于点
轴于点 ,延长
,延长 交
交 于点
于点 ,若
,若 ,
, ,求点
,求点 的坐标.
的坐标.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
 为圆心的⊙P经过(-2, 0)以1个单位/秒的速度沿
为圆心的⊙P经过(-2, 0)以1个单位/秒的速度沿  轴向右运动,则当
轴向右运动,则当  与
与  轴相交的弦长为4时,则移动的时间为( )
轴相交的弦长为4时,则移动的时间为( )
A.2秒
B.3秒
C.2秒或4秒
D.3秒或6秒[来
相关试题

