【题目】如图1,等腰![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,
,![]()
(1)求证:![]() 是等边三角形
是等边三角形
(2)如图2,在![]() 内有一点
内有一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的度数
的度数
(3)如图3,在(2)的条件下,在![]() 外有一点
外有一点![]() ,连接
,连接![]() 、
、![]() 、若
、若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.



参考答案:
【答案】(1)证明见解析,(2)150°;(3)6.
【解析】
(1)构造△CDE≌△BDA,可得∠E=∠CAD=∠BAD, AC=EC,故AB=EC=AC=BC,即可解答.
(2)以AD为边作等边△ADE,连接EC,易证△ABD≌ACE,EC=BD,由已知可得Rt△EDC,从而∠ADC=60°+90°=150°;
(3)作2倍角的平分线构造全等三角形,Rt△AGC≌Rt△AHC≌Rt△AHF;由∠ADC=150°可得∠CDG=30°,可知CG=CH=HF=![]() CD,从而得到△CEF为等腰三角形,由△CFE∽△ACF可得
CD,从而得到△CEF为等腰三角形,由△CFE∽△ACF可得![]() ,即可计算AF长,由AF=AC=AB即可解答.
,即可计算AF长,由AF=AC=AB即可解答.
(1)证明:延长AD到E,使DE=AD,
在△CDE和△ABD中

∴△CDE≌△BDA(SAS)
∴∠E=∠BAD,AB=CE,
∵AB=BC,
∴∠BAC=∠C,
又∵![]() ,∠BAC=∠BAD+CAD,
,∠BAC=∠BAD+CAD,
∴∠E=∠CAD,
∴AC=CE,
∴AC=AB=BC,即![]() 是等边三角形
是等边三角形

(2)以AD为边作等边△ADE,连接EC,

∵∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△AEC中,

∴△ABD≌△ACE(SAS)
∴EC=BD,
在等边三角形ADE中,AD=DE,∠ADE=60°,
∵![]() ,
,
∴![]() ,
,
∴∠EDC=90°,
∴∠ADC=∠ADE+∠EDC=60°+90°=150°
(3)作∠CAE平分线AH,过C点作CG⊥AD交AD延长线于G点,作CH⊥AH交AH于H点,交AE延长线与F点,

由(2)得,∠ADC=150°,
∴∠CDG=30°,
∴CG=![]() CD,
CD,
∵∠CAE=2∠CAD,
∴∠CAG=∠CAH,
又∵CG⊥AD, CH⊥AH,易证△AGC≌△AHC≌△AHF;
∴GC=HC=HF,∠ACF=∠F,AB=AF,
∵CD=CE,CF=2CG=CD,
∴CE=CF,
∴∠CEF=∠EFC,
又∵∠F=∠F,
∴△CFE∽△ACF
∴![]() ,
,
∵AE=4,CE=CF=2![]() ,AF=4+EF
,AF=4+EF
∴EF=2,
∴AB=AC=AF=4+2=6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
 、
、 在
在 的边
的边 上,
上, ,
, ,
,(1)求证:

(2)如图2,若
 ,
, ,
, ,求线段
,求线段 的长
的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:
单价(元/件)
25
28
35
40
42
销量(件)
50
44
30
20
16
(1)通过对上面表格中的数据进行分析,发现销量y(件)与单价x(元/件)之间存在一次函数关系,求y关于x的函数关系式(不需要写出函数自变量的取值范围);
(2)预计在今后的销售中,销量与单价仍然存在(1)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),
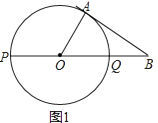
(1)当线段AB所在的直线与圆O相切时,求弧AQ的长(图1);
(2)若∠AOB=120°,求AB的长(图2);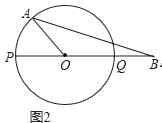
(3)如果线段AB与圆O有两个公共点A、M,当AO⊥PM于点N时,求tan∠MPQ的值(图3).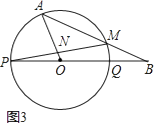
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,ABCD的顶点的坐标分别为A(﹣6,9),B(0,9),C(3,0),D(﹣3,0),抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)过A、B两点,顶点为M.

(1)若抛物线过点C,求抛物线的解析式;
(2)若抛物线的顶点M落在△ACD的内部(包括边界),求a的取值范围;
(3)若a<0,连结CM交线段AB于点Q(Q不与点B重合),连接DM交线段AB于点P,设S1=S△ADP+S△CBQ , S2=S△MPQ , 试判断S1与S2的大小关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图一,点
 在线段
在线段 上,图中有三条线段
上,图中有三条线段 、
、 和
和 ,若其中一条线段的长度是另外一条线段长度的
,若其中一条线段的长度是另外一条线段长度的 倍,则称点
倍,则称点 是线段
是线段 的“巧点”.
的“巧点”.(1)填空:线段的中点 这条线段的巧点(填“是”或“不是”或“不确定是”)
(问题解决)
(2)如图二,点
 和
和 在数轴上表示的数分别是
在数轴上表示的数分别是 和
和 ,点
,点 是线段
是线段 的巧点,求点
的巧点,求点 在数轴上表示的数。
在数轴上表示的数。(应用拓展)
(3)在(2)的条件下,动点
 从点
从点 处,以每秒
处,以每秒 个单位的速度沿
个单位的速度沿 向点
向点 匀速运动,同时动点
匀速运动,同时动点 从点
从点 出发,以每秒
出发,以每秒 个单位的速度沿
个单位的速度沿 向点
向点 匀速运动,当其中一点到达中点时,两个点运动同时停止,当
匀速运动,当其中一点到达中点时,两个点运动同时停止,当
、  、
、 三点中,其中一点恰好是另外两点为端点的线段的巧点时,直接写出运动时间
三点中,其中一点恰好是另外两点为端点的线段的巧点时,直接写出运动时间 的所有可能值.
的所有可能值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
 的边长为
的边长为  ,
,  ,弧
,弧  是以点
是以点  为圆心、
为圆心、  长为半径的弧,弧
长为半径的弧,弧  是以点
是以点  为圆心、
为圆心、  长为半径的弧,则阴影部分的面积为( )
长为半径的弧,则阴影部分的面积为( )
A.
B.
C.
D.
相关试题

