【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),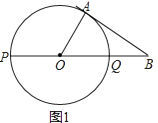
(1)当线段AB所在的直线与圆O相切时,求弧AQ的长(图1);
(2)若∠AOB=120°,求AB的长(图2);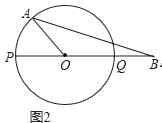
(3)如果线段AB与圆O有两个公共点A、M,当AO⊥PM于点N时,求tan∠MPQ的值(图3).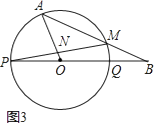
参考答案:
【答案】
(1)解:∵直线AB与圆O相切,
∴∠OAB=90°,
∵OQ=QB=1,
∴OA=1,OB=2,
∴OA= ![]() OB,
OB,
∴∠B=30°,
∴∠AOB=60°,
∴AQ= ![]() ;
;
(2)解:如图1, 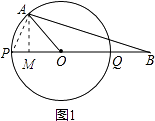
连接AP,过点A作AM⊥BP于M,
∵∠AOB=120°,
∴∠AOP=60°,
∵sin∠AOP= ![]() ,
,
∴AM=sin∠AOPAO=sin60°×1= ![]() ,
,
∵OM= ![]() ,
,
∴BM=OM+OB= ![]() +2=
+2= ![]() ,
,
∴AB= ![]() ;
;
(3)解:如图2,连接MQ,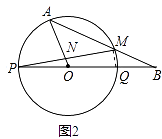
∵PQ为圆O的直径,
∴∠PMQ=90°,
∵ON⊥PM,
∴AO∥MQ,
∵PO=OQ,
∴ON= ![]() MQ,
MQ,
∵OQ=BQ,
∴MQ= ![]() AO,
AO,
∴ON= ![]() AO,
AO,
设ON=x,则AO=4x,
∵OA=1,
∴4x=1,
∴x= ![]() ,
,
∴ON= ![]() ,
,
∴PN= ![]() ,
,
∴tan∠MPQ= 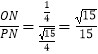 .
.
【解析】(1)先根据直角三角形的性质求出∠B的度数,得到∠AOB的度数,再根据弧长的计算公式进行求解即可。
(2)连接AP,过点A作AM⊥BP于M,根据特殊角的三角函数值和已知条件求出AM,再根据BM=OM+OB,求出BM,最后根据勾股定理求出AB。
(3)连接MQ,先根据PQ是圆O的直径和AO⊥PM,得出ON∥MQ,求出ON与OA的数量关系,设ON=x,则AO=4x,根据OA的值求出x的值,再根据勾股定理求出PN的长,最后根据三角函数的定义即可得出答案。
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径,以及对弧长计算公式的理解,了解若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售
 两种商品,每件的售价分别为
两种商品,每件的售价分别为 元、
元、 元,五一期间,该商店决定对这两种商品进行促销活动,如图所示,若小红打算到该商店购买
元,五一期间,该商店决定对这两种商品进行促销活动,如图所示,若小红打算到该商店购买 件
件 商品和
商品和 件
件 商品,根据以上信息,请:
商品,根据以上信息,请:
(1)分别用含的代数式表示按照方案一和方案二所需的费用
 和
和 ;
;(2)就
 的不同取值,请说明选择那种方案购买更实惠(两种优惠方案不能同时享受)
的不同取值,请说明选择那种方案购买更实惠(两种优惠方案不能同时享受) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
 、
、 在
在 的边
的边 上,
上, ,
, ,
,(1)求证:

(2)如图2,若
 ,
, ,
, ,求线段
,求线段 的长
的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:
单价(元/件)
25
28
35
40
42
销量(件)
50
44
30
20
16
(1)通过对上面表格中的数据进行分析,发现销量y(件)与单价x(元/件)之间存在一次函数关系,求y关于x的函数关系式(不需要写出函数自变量的取值范围);
(2)预计在今后的销售中,销量与单价仍然存在(1)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等腰
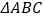 中,
中, ,
, 为
为 中点,连接
中点,连接 ,
,
(1)求证:
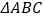 是等边三角形
是等边三角形(2)如图2,在
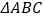 内有一点
内有一点 ,连接
,连接 、
、 、
、 ,若
,若 ,求
,求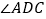 的度数
的度数(3)如图3,在(2)的条件下,在
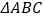 外有一点
外有一点 ,连接
,连接 、
、 、若
、若 ,
, ,
, ,求线段
,求线段 的长.
的长.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,ABCD的顶点的坐标分别为A(﹣6,9),B(0,9),C(3,0),D(﹣3,0),抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)过A、B两点,顶点为M.

(1)若抛物线过点C,求抛物线的解析式;
(2)若抛物线的顶点M落在△ACD的内部(包括边界),求a的取值范围;
(3)若a<0,连结CM交线段AB于点Q(Q不与点B重合),连接DM交线段AB于点P,设S1=S△ADP+S△CBQ , S2=S△MPQ , 试判断S1与S2的大小关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图一,点
 在线段
在线段 上,图中有三条线段
上,图中有三条线段 、
、 和
和 ,若其中一条线段的长度是另外一条线段长度的
,若其中一条线段的长度是另外一条线段长度的 倍,则称点
倍,则称点 是线段
是线段 的“巧点”.
的“巧点”.(1)填空:线段的中点 这条线段的巧点(填“是”或“不是”或“不确定是”)
(问题解决)
(2)如图二,点
 和
和 在数轴上表示的数分别是
在数轴上表示的数分别是 和
和 ,点
,点 是线段
是线段 的巧点,求点
的巧点,求点 在数轴上表示的数。
在数轴上表示的数。(应用拓展)
(3)在(2)的条件下,动点
 从点
从点 处,以每秒
处,以每秒 个单位的速度沿
个单位的速度沿 向点
向点 匀速运动,同时动点
匀速运动,同时动点 从点
从点 出发,以每秒
出发,以每秒 个单位的速度沿
个单位的速度沿 向点
向点 匀速运动,当其中一点到达中点时,两个点运动同时停止,当
匀速运动,当其中一点到达中点时,两个点运动同时停止,当
、  、
、 三点中,其中一点恰好是另外两点为端点的线段的巧点时,直接写出运动时间
三点中,其中一点恰好是另外两点为端点的线段的巧点时,直接写出运动时间 的所有可能值.
的所有可能值.
相关试题

