Question

【题目】如图1，在平面直角坐标系中，点在轴正半轴，点在轴负半轴，连接，，

（1）求点坐标

（2）如图2，点是线段上一点，连接，以为直角边做等腰直角，，设点的横坐标为，求点的坐标（用含的代数式表示）

（3）在（2）的条件下，如图3，在延长线上有一点，过点作的平行线，交轴于点，延长交于点，若，，求点的坐标.

Answer 1

【答案】(1) 点B坐标为（-2，0）,(2) 点E的坐标（2-m，m），(3)F点（1，3）.

【解析】

（1）根据△AOB是等腰直角三角形可求出OA、OB长，即可得到B的坐标；

（2）作DM⊥OB，EN⊥X轴，垂足分别为M、N，易证△DOM≌△OEN，从而DM=ON,OM=EN，即可得到E点坐标；

（3）延长OD交HF延长线于P点，在y轴正半轴取R点使OR=OH，过F点作FM垂直于y轴，将AF=GH转化为MF=GH=PR，再利用△RNP≌△FNM，△BOD≌△PFD，得PF=MR=OB=2, 设MF=m，MN=y，FN=2-y，则MA=m，OH=OR=4+m，用勾股定理和相似列方程组解出m即可解答.

解：（1）∵∠ABO=45°，

∴△AOB是等腰直角三角形，

∴2OB2=AB2，

∵AB=2

∴OB=2，

∴点B坐标为（-2，0）

（2）作DM⊥OB，EN⊥X轴，垂足分别为M、N，

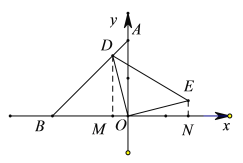
∵∠DOE=90°，

∴∠MDO=∠NOE，

在△DOM和△OEN中

,

∴△DOM≌△OEN（AAS）

∴DM=ON,OM=EN

∵△BMD、△BOA是等腰直角三角形，EN=OM=-m

∴ON=DM=2+m

∴点E的坐标（2+m，-m），

（3）延长OD交HF延长线于P点，在y轴正半轴取R点使OR=OH，过F点作FM垂直于y轴，

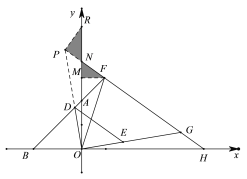
∵△DOE是等腰直角三角形，DE∥FH，

∴△POG是等腰直角三角形，

易证△POR≌△GOH，

∴PR=GH，∠PRN=∠GHO

∵MF⊥y轴，△AOB是等腰直角三角形，

∴△AMF是等腰直角三角形，∠GHO=∠NFM

∴AF=MF，

又∵AF=GH

∴PR=GH=MF，

在△RNP和△FNM中

,

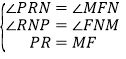△RNP≌△FNM（AAS）

∴PN=MN，FN=RN，

∴PF=MR

在△BOD和△PFD中，

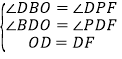
∴△BOD≌△PFD（AAS），

∴PF=OB=MR=2，

设MF=m，MN=y，FN=2-y，则MA=m，OH=OR=4+m

在Rt△MNF中，，

∴，

∵△MFN∽△OHN

∴，

∴，

联立解方程得m=1，

∴F点坐标为（1，3）