【题目】学完“证明(二)”一章后,老师布置了一道思考题:如图,点M、N分别在正三角形ABC的边BC.CA上,且BM=CN,AM、BN交于点Q。求证:∠BQM=60°。
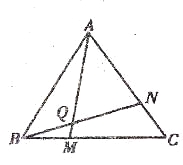
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?
③若将题中的条件“点M,N分别在正三角形ABC的BC、CA边上”改为“点M,N分别在正方形ABCD的BC,CD边上”,是否仍能得到∠BQM=60°?对②,③进行证明。(自己画出对应的图形)
参考答案:
【答案】(1)见解析;(2)①是;②是;③否
【解析】
试题(1)根据正三角形的性质可得AB=BC,∠ABM=∠BCN,再结合BM=CN根据“SAS”可证得△ABM![]() △BCN,可得∠BAM=∠CBN,即可求得结果;
△BCN,可得∠BAM=∠CBN,即可求得结果;
(2)①仍为真命题;②易证△BAN![]() △ACM(SAS),可得∠1=∠2,∠N=∠M,即可求得结果;
△ACM(SAS),可得∠1=∠2,∠N=∠M,即可求得结果;
③易证△ABM![]() △BCN(SAS),可得∠1=∠2,又∠2+∠3=90°,即得∠BQM=∠1+∠3=∠2+∠3=90°.
△BCN(SAS),可得∠1=∠2,又∠2+∠3=90°,即得∠BQM=∠1+∠3=∠2+∠3=90°.
(1)∵正三角形ABC
∴AB=BC,∠ABM=∠BCN
∵BM=CN
∴△ABM![]() △BCN(SAS)
△BCN(SAS)
∴∠BAM=∠CBN,
∴∠BQM=∠BAQ+∠ABQ=∠MBQ+∠ABQ=60°;
(2)①仍为真命题;
②如图:
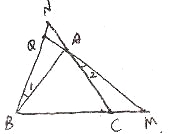
易证△BAN![]() △ACM(SAS)
△ACM(SAS)
∴∠1=∠2,∠N=∠M
又∠BQM=∠N+∠QAN=∠N+∠2=∠M+∠2=∠ACB=60°;
③如图
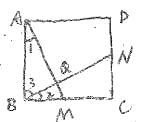
此时不能得到∠BQM=60°,而有∠BQM=90°
易证△ABM![]() △BCN(SAS)
△BCN(SAS)
∴∠1=∠2,又∠2+∠3=90°,
∴∠BQM=∠1+∠3=∠2+∠3=90°.
-
科目: 来源: 题型:
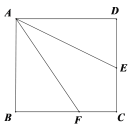
查看答案和解析>>【题目】如图,已知E是正方形ABCD的边CD的中点,点F在BC上,且∠DAE=∠FAE,
求证:AF=AD+CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1=
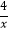 的图象经过点B;反比例函数y2=
的图象经过点B;反比例函数y2=  的图象经过点C(
的图象经过点C(  ,m).
,m).
(1)求点B的坐标;
(2)△ABC的内切圆⊙M与BC,CA,AB分别相切于D,E,F,求圆心M的坐标. -
科目: 来源: 题型:
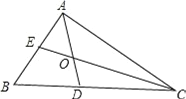
查看答案和解析>>【题目】如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,
(1)求∠AOC的度数;
(2)求证:OE=OD;
(3).猜测AE,CD,AC三者的数量关系,并证明.
-
科目: 来源: 题型:
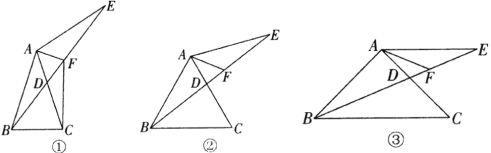
查看答案和解析>>【题目】如图,在等腰三角形
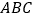 中,
中,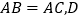 是
是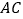 上一动点,点
上一动点,点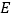 在
在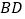 的延长线上,且
的延长线上,且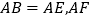 平分
平分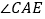 ,交
,交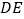 于点
于点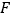 .
.(1)如图①,连接
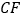 ,求证:
,求证:  ;
;(2)如图②,当
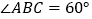 时,求证:
时,求证: 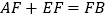 ;
;(3)如图③,当
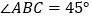 时,若
时,若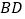 平分
平分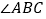 ,求证:
,求证:  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出ΔAPC≌ΔAPD的是( )

A.BC=BD B.∠ACB=∠ADB C.AC=AD D.∠CAB=∠DAB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
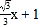 交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的面积是__.
交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的面积是__.
相关试题

