【题目】如图,在平面直角坐标系中,点O为坐标原点,△ABC是直角三角形,∠ACB=90°,点B、C都在第一象限内,CA⊥x轴,垂足为点A,反比例函数y1= ![]() 的图象经过点B;反比例函数y2=
的图象经过点B;反比例函数y2= ![]() 的图象经过点C(
的图象经过点C( ![]() ,m).
,m).
(1)求点B的坐标;
(2)△ABC的内切圆⊙M与BC,CA,AB分别相切于D,E,F,求圆心M的坐标.
参考答案:
【答案】
(1)
解:∵CA⊥x轴,∠ACB=90°,
∴CB∥x轴.
∵将C( ![]() ,m)代入函数y2=
,m)代入函数y2= ![]() 得:n=
得:n= ![]() =
= ![]() ,
,
∴点C( ![]() ,
, ![]() ).
).
∴点B的纵坐标为 ![]() .
.
∵将y1= ![]() 代入得:
代入得: ![]() =
= ![]() ,解得;x=2
,解得;x=2 ![]() ,
,
∴点B的坐标为(2 ![]() ,
, ![]() )
)
(2)
解:如图所示:连接ME、MD、MF.
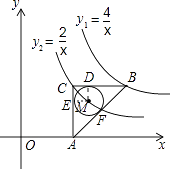
∵⊙M与BC,CA,AB分别相切于D,E,F,
∴ME⊥AC,MD⊥BC,MF⊥AB.
∴∠ECD=∠CDM=∠CEM=90°.
∴四边形CDME为矩形.
∵MD=ME,
∴四边形CDME为正方形.
∵在Rt△ACB中,AC= ![]() ,BC=
,BC= ![]() ,
,
∴AB=2.
∵S△ACB= ![]() ACBC=
ACBC= ![]() (AC+BC+AB)r,
(AC+BC+AB)r,
∴⊙M的半径= ![]() =
= ![]() =
= ![]() ﹣1.
﹣1.
∴点M的坐标为(2 ![]() ﹣1,1)
﹣1,1)
【解析】(1)先求得点C的坐标,然后根据平行于x轴上点纵坐标相等,可知点B的纵坐标,然后可求得点B的横坐标;(2)连接MD、ME、MF.由点B和点C的坐标可求得AC、BC的长,依据勾股定理可求得AB的长,然后在△ABC中利用面积法可求得圆M的半径,从而可求得点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,△AOB为顶点A,B的坐标分别为A(0,4),B(﹣3,0),按要求解答下列问题.

(1)①在图中,先将△AOB向上平移6个单位,再向右平移3个单位,画出平移后的△A1O1B1;(其中点A,O,B的对应点为A1 , O1 , B1)
②在图中,将△A1O1B1绕点O1顺时针旋转90°,画出旋转后的Rt△A2O1B2;(其中点A1 , B1的对应点为A2 , B2)
(2)直接写出点A2 , B2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在新晚报举办的“万人户外徒步活动”中,为统计参加活动人员的年龄情况,从参加人员中随机抽取了若干人的年龄作为样本,进行数据统计,制成如图的条形统计图和扇形统计图(部分).

(1)本次活动统计的样本容量是多少?
(2)求本次活动中70岁以上的人数,并补全条形统计图;
(3)本次参加活动的总人数约为12000人,请你估算参加活动人数最多的年龄段的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E是正方形ABCD的边CD的中点,点F在BC上,且∠DAE=∠FAE,
求证:AF=AD+CF.
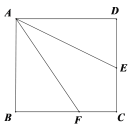
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,
(1)求∠AOC的度数;
(2)求证:OE=OD;
(3).猜测AE,CD,AC三者的数量关系,并证明.
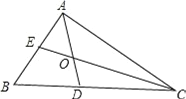
-
科目: 来源: 题型:
查看答案和解析>>【题目】学完“证明(二)”一章后,老师布置了一道思考题:如图,点M、N分别在正三角形ABC的边BC.CA上,且BM=CN,AM、BN交于点Q。求证:∠BQM=60°。
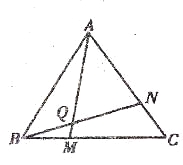
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?
③若将题中的条件“点M,N分别在正三角形ABC的BC、CA边上”改为“点M,N分别在正方形ABCD的BC,CD边上”,是否仍能得到∠BQM=60°?对②,③进行证明。(自己画出对应的图形)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形
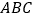 中,
中,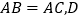 是
是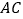 上一动点,点
上一动点,点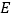 在
在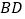 的延长线上,且
的延长线上,且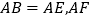 平分
平分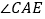 ,交
,交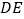 于点
于点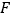 .
.(1)如图①,连接
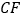 ,求证:
,求证:  ;
;(2)如图②,当
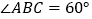 时,求证:
时,求证: 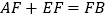 ;
;(3)如图③,当
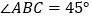 时,若
时,若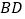 平分
平分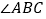 ,求证:
,求证:  .
.
相关试题

