【题目】如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出ΔAPC≌ΔAPD的是( )

A.BC=BD B.∠ACB=∠ADB C.AC=AD D.∠CAB=∠DAB
参考答案:
【答案】C
【解析】
试题分析:选项A,补充BC=BD,利用SAS先证出△ABC≌△ABD,可得∠CAB=∠DAB,AC=AD,再利用SAS即可得△APC≌△APD,选项A正确;选项B,补充∠ACB=∠ADB,利用AAS先证出△ABC≌△ABD,可得∠CAB=∠DAB,AC=AD,再利用SAS即可得△APC≌△APD,选项B正确;选项C,补充AC=AD,不能推出△APC≌△APD,选项C错误;选项D,补充∠CAB=∠DAB,利用ASA先证出△ABC≌△ABD,可得AC=AD,再利用SAS即可得△APC≌△APD,选项D正确.故答案选C.
-
科目: 来源: 题型:
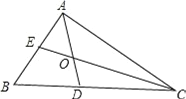
查看答案和解析>>【题目】如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,
(1)求∠AOC的度数;
(2)求证:OE=OD;
(3).猜测AE,CD,AC三者的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学完“证明(二)”一章后,老师布置了一道思考题:如图,点M、N分别在正三角形ABC的边BC.CA上,且BM=CN,AM、BN交于点Q。求证:∠BQM=60°。
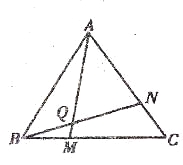
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?
③若将题中的条件“点M,N分别在正三角形ABC的BC、CA边上”改为“点M,N分别在正方形ABCD的BC,CD边上”,是否仍能得到∠BQM=60°?对②,③进行证明。(自己画出对应的图形)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形
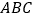 中,
中,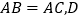 是
是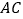 上一动点,点
上一动点,点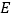 在
在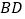 的延长线上,且
的延长线上,且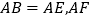 平分
平分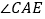 ,交
,交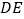 于点
于点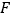 .
.(1)如图①,连接
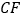 ,求证:
,求证:  ;
;(2)如图②,当
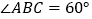 时,求证:
时,求证: 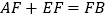 ;
;(3)如图③,当
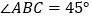 时,若
时,若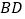 平分
平分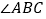 ,求证:
,求证:  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y=
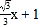 交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的面积是__.
交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的面积是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发.设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地时间为x(h),y甲、y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h.
(2)请分别求出y甲、y乙与x之间的函数关系式.
(3)当乙与A地相距240km时,甲与B地相距多少千米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.
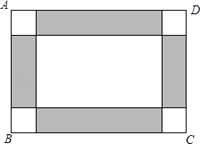
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?
相关试题

