【题目】如图,AB是⊙O的直径,C,P是 ![]() 上两点,AB=13,AC=5.
上两点,AB=13,AC=5. 
(1)如图(1),若点P是 ![]() 的中点,求PA的长;
的中点,求PA的长;
(2)如图(2),若点P是 ![]() 的中点,求PA的长.
的中点,求PA的长.
参考答案:
【答案】
(1)解:如图(1)所示,连接PB,

∵AB是⊙O的直径且P是 ![]() 的中点,
的中点,
∴∠PAB=∠PBA=45°,∠APB=90°,
又∵在等腰三角形△APB中有AB=13,
∴PA= ![]() =
= ![]() =
= ![]()
(2)解:如图(2)所示:连接BC.OP相交于M点,作PN⊥AB于点N,

∵P点为弧BC的中点,
∴OP⊥BC,∠OMB=90°,
又因为AB为直径
∴∠ACB=90°,
∴∠ACB=∠OMB,
∴OP∥AC,
∴∠CAB=∠POB,
又因为∠ACB=∠ONP=90°,
∴△ACB∽△0NP
∴ ![]() =
= ![]() ,
,
又∵AB=13 AC=5 OP= ![]() ,
,
代入得 ON= ![]() ,
,
∴AN=OA+ON=9
∴在Rt△OPN中,有NP2=0P2﹣ON2=36
在Rt△ANP中 有PA= ![]() =
= ![]() =3
=3 ![]()
∴PA=3 ![]()
【解析】(1)根据圆周角的定理,∠APB=90°,P是弧AB的中点,所以三角形APB是等腰三角形,利用勾股定理即可求得.(2)根据垂径定理得出OP垂直平分BC,得出OP∥AC,从而得出△ACB∽△0NP,根据对应边成比例求得ON、AN的长,利用勾股定理求得NP的长,进而求得PA.
【考点精析】本题主要考查了等腰直角三角形和勾股定理的概念的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期
一
二
三
四
五
六
日
增减/吨
﹣1
+3
﹣2
+4
+7
﹣5
﹣10
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车油箱的容积为70升,小王把油箱注满油后准备驾驶汽车从县城到300千米外的省城接待客人,在接到客人后立即按原路返回,请回答下列问题:
(1)油箱注满油后,汽车能够行使的总路程y(单位:千米)与平均耗油量x(单位:升/千米)之间有怎样的函数关系?
(2)如果小王以平均每千米耗油0.1升的速度驾驶汽车到达省城,在返程时由于下雨,小王降低了车速,此时每行驶1千米的耗油量增加了一倍,如果小王一直以此速度行驶,邮箱里的油是否够回到县城?如果不够用,至少还需加多少油? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点. (Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.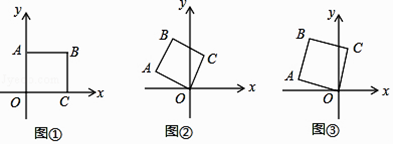
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+2xa+c经过A(﹣4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.

(1)求抛物线的解析式;
(2)点P是第二象限抛物线上的一个动点,连接EP,过点E作EP的垂线l,在l上截取线段EF,使EF=EP,且点F在第一象限,过点F作FM⊥x轴于点M,设点P的横坐标为t,线段FM的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点E作EH⊥ED交MF的延长线于点H,连接DH,点G为DH的中点,当直线PG经过AC的中点Q时,求点F的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,
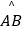 =
= 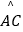 ,∠AOB=40°,则∠ADC的度数是( )
,∠AOB=40°,则∠ADC的度数是( ) 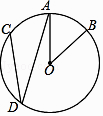
A.15°
B.20°
C.30°
D.40°
相关试题

