【题目】我们规定:在正方形ABCD中,以正方形的一个顶点A为顶点,且过对角顶点C的抛物线,称为这个正方形的以A为顶点的对角抛物线.
(1)在平面直角坐标系xOy中,点在轴正半轴上,点C在y轴正半轴上.
①如图1,正方形OABC的边长为2,求以O为顶点的对角抛物线;
②如图2,在平面直角坐标系xOy中,正方形OABC的边长为a,其以O为顶点的对角抛物线的解析式为y= ![]() x2 , 求a的值;
x2 , 求a的值;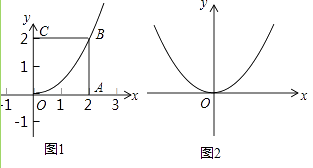
(2)如图3,正方形ABCD的边长为4,且点A的坐标为(3,2),正方形的四条对角抛物线在正方形ABCD内分别交于点M、P、N、Q,直接写出四边形MPNQ的形状和四边形MPNQ的对角线的交点坐标.
参考答案:
【答案】
(1)
解:①如图1中,设O为顶点的抛物线的解析式为y=ax2,
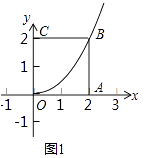
∵过B(2,2),
∴2=4a,
∴a= ![]() ,
,
∴所求的抛物线的解析式为y= ![]() x2.
x2.
②如图2中,设B(a,a).
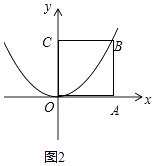
则有a= ![]() a2,解得a=4或0(舍弃),
a2,解得a=4或0(舍弃),
∴B(4,4),
∴OA=4,
∴正方形的边长为4
(2)
解:如图3中,结论:四边形MPNQ是菱形,对角线的交点坐标为(5,4).
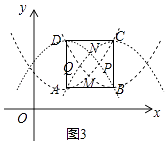
理由:∵正方形ABCD的边长为4,A(3,2),
∴B(7,2),C(7,6),D(3,6),
∴以A为顶点的对角抛物线为y= ![]() (x﹣3)2+2,
(x﹣3)2+2,
以B为顶点的对角抛物线为y= ![]() (x﹣7)2+2,
(x﹣7)2+2,
以C为顶点的对角抛物线为y=﹣ ![]() (x﹣7)2+6,
(x﹣7)2+6,
以D为顶点的对角抛物线为y=﹣ ![]() (x﹣3)2+6,
(x﹣3)2+6,
由 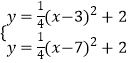 可得M(5,3),
可得M(5,3),
由 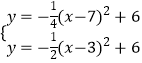 可得N(5,5),
可得N(5,5),
由 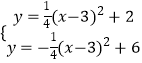 可得P(3+2
可得P(3+2 ![]() ,4),
,4),
由 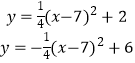 可得Q(7﹣2
可得Q(7﹣2 ![]() ,4),
,4),
∴PM= ![]() ,
,
PN= ![]() ,
,
QN= ![]() ,
,
QM= ![]() ,
,
∴PM=PN=QN=QM,
∴四边形MPNQ是菱形,对角线的交点坐标为(5,5)
【解析】(1)①设O为顶点的抛物线的解析式为y=ax2 , 把B(2,2)代入即可解决问题.②设B(a,a).代入y= ![]() x2求出a即可解决问题.(2)如图3中,结论:四边形MPNQ是菱形,对角线的交点坐标为(5,4).求出A、B、C、D的顶点的对角抛物线,利用方程组求出M、P、N、Q的坐标即可解决问题.
x2求出a即可解决问题.(2)如图3中,结论:四边形MPNQ是菱形,对角线的交点坐标为(5,4).求出A、B、C、D的顶点的对角抛物线,利用方程组求出M、P、N、Q的坐标即可解决问题.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=-
 x,点A1的坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,则点A3的坐标为________,按此作法进行下去,点A2017的坐标为__________.
x,点A1的坐标为(-3,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,则点A3的坐标为________,按此作法进行下去,点A2017的坐标为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个“有理数转换器”(箭头是指有理数进入转换器后的路径,方框是对进入的数进行转换的转换器)
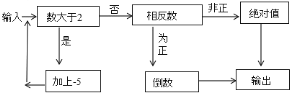
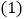 当小明输入
当小明输入 ;
; ;
;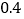 这三个数时,这三次输入的结果分别是多少?
这三个数时,这三次输入的结果分别是多少?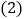 你认为当输入什么数时,其输出的结果是
你认为当输入什么数时,其输出的结果是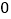 ?
? 你认为这的“有理数转换器”不可能输出什么数?
你认为这的“有理数转换器”不可能输出什么数? -
科目: 来源: 题型:
查看答案和解析>>【题目】一股民上星期五买进某公司股票
 股,每股
股,每股 元,下表为本周内每日该股票的涨跌情况(单位:元)
元,下表为本周内每日该股票的涨跌情况(单位:元)星期
一
二
三
四
五
每股涨跌
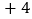




 星期三收盘时,每股是________元;
星期三收盘时,每股是________元; 本周内每股最高价为________元,每股最低价为________元;
本周内每股最高价为________元,每股最低价为________元; 已知该股民买进股票时付了
已知该股民买进股票时付了 ‰的手续费,卖出时还需付成交额
‰的手续费,卖出时还需付成交额 ‰的手续费和
‰的手续费和 ‰的交易锐,如果该股民在星期五收盘前将全部股票卖出,他的收益情况如何?
‰的交易锐,如果该股民在星期五收盘前将全部股票卖出,他的收益情况如何? -
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D﹣d.
(1)①如图1,在平面直角坐标系xOy中,图形G1为以O为圆心,2为半径的圆,直接写出以下各点到图形G1的距离跨度:
A(﹣1,0)的距离跨度;
B( ,﹣
,﹣  )的距离跨度;
)的距离跨度;
C(﹣3,2)的距离跨度;
②根据①中的结果,猜想到图形G1的距离跨度为2的所有的点组成的图形的形状是 .
(2)如图2,在平面直角坐标系xOy中,图形G2为以C(1,0)为圆心,2为半径的圆,直线y=k(x+1)上存在到G2的距离跨度为2的点,求k的取值范围.
(3)如图3,在平面直角坐标系xOy中,射线OA:y= x(x≥0),圆C是以3为半径的圆,且圆心C在x轴上运动,若射线OA上存在点到圆C的距离跨度为2,直接写出圆心C的横坐标xc的取值范围.
x(x≥0),圆C是以3为半径的圆,且圆心C在x轴上运动,若射线OA上存在点到圆C的距离跨度为2,直接写出圆心C的横坐标xc的取值范围. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点A(0,2)和点B(-a,3),且点B在正比例函数y=-3x的图象上.
(1)求a的值;
(2)求一次函数的解析式并画出它的图象;
(3)若P(m,y1),Q(m-1,y2)是这个一次函数图象上的两点,试比较y1与y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数关系的图像.
(1)他们出发半小时后,离家多少千米?
(2)求出AB段的函数表达式.

相关试题

