【题目】已知一次函数y=kx+b的图象经过点A(0,2)和点B(-a,3),且点B在正比例函数y=-3x的图象上.
(1)求a的值;
(2)求一次函数的解析式并画出它的图象;
(3)若P(m,y1),Q(m-1,y2)是这个一次函数图象上的两点,试比较y1与y2的大小.
参考答案:
【答案】(1)a=1;(2)y=-x+2.(3)y1<y2.
【解析】试题分析:(1)把B点坐标代入正比例函数解析式即可求出![]() 的值;
的值;
(2)把点A和B点坐标分别代入y=kx+b得到关于k和b的方程组,然后解方程组求出k和b,从而得到一次函数解析式,再利用描点法画出一次函数的图象;
(3)根据一次函数的性质求解.
试题解析:(1)∵点B(-a,3)在正比例函数y=-3x的图象上,
∴3=-3×(-a),
∴a=1;
(2)由(1)可得点B的坐标为(-1,3),将(-1,3)和(0,2)代入y=kx+b中,
得b=2,-k+b=3,解得k=-1,∴一次函数的解析式为y=-x+2.
图象如图所示:
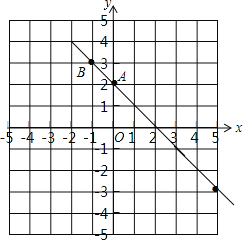
(3)∵-1<0,∴y随x的增大而减小.
又∵m>m-1,∴y1<y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校需购买一批课桌椅供学生使用,已知A型课桌椅230元/套,B型课桌椅200元/套.
(1)该校购买了A,B型课桌椅共250套,付款53000元,求A,B型课桌椅各买了多少套?
(2)因学生人数增加,该校需再购买100套A,B型课桌椅,现只有资金22000元,最多能购买A型课桌椅多少套? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为
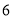 的正三角形纸片
的正三角形纸片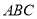 按如下顺序进行两次折叠,展开后,得折痕
按如下顺序进行两次折叠,展开后,得折痕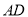 ,
,  (如图①),点
(如图①),点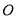 为其交点.
为其交点.(
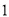 )探求
)探求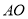 到
到 的数量关系,并说明理由.
的数量关系,并说明理由.(
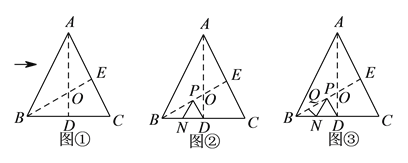
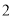 )如图②,若
)如图②,若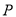 ,
, 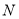 分别为
分别为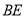 ,
, 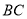 上的动点.
上的动点.①当
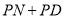 的长度取得最小值时,求
的长度取得最小值时,求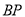 的长度.
的长度.②如图③,若点
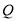 在线段
在线段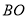 上,
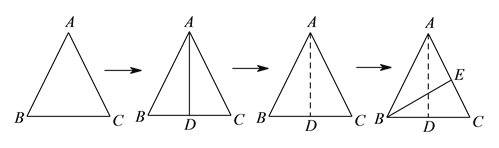
上,  ,则
,则 的最小值
的最小值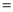 __________.
__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题: 学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2
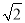 =(1+
=(1+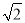 )2, 我们来进行以下的探索:
)2, 我们来进行以下的探索:设a+b
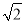 =(m+n
=(m+n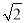 )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b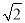 =m2+2n2+2mn
=m2+2n2+2mn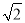 ,∴a=m+2n2 , b=2mn, 这样就得出了把类似a+b
,∴a=m+2n2 , b=2mn, 这样就得出了把类似a+b 的式子化为平方式的方法.
的式子化为平方式的方法.请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都为正整数时,若a﹣b
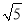 =(m﹣n
=(m﹣n )2 , 用含m,n的式子分别表示a,b,得a=________,b=________;
)2 , 用含m,n的式子分别表示a,b,得a=________,b=________; (2)利用上述方法,找一组正整数a,b,m,n填空:___﹣_____
 =(____﹣_____
=(____﹣_____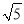 )2
)2 (3)a﹣4
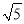 =(m﹣n
=(m﹣n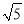 )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于D,E为
 的中点,连接CE,BE,BE交AC于F.
的中点,连接CE,BE,BE交AC于F. 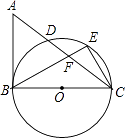
(1)求证:AB=AF;
(2)若AB=3,BC=4,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式中,含有因式
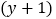 的多项式是( )
的多项式是( )A.
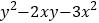 B.
B. 
C.
 D.
D. 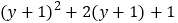
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)(1+a)(1-a)+(a-2)2,其中a=
 ;
;(2)(2x+3)(2x-3)-4x(x-1)+(x-2)2,其中x=-3.
相关试题

