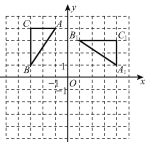
【题目】如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4),B(-3,1),C(-3,4),△A1B1C1是由△ABC绕某一点旋转得到的.
(1)请直接写出旋转中心的坐标是________,旋转角是_____°;
(2)将△ABC平移得到△A2B2C2,使得点A2的坐标为(0,-1),请画出平移后的△A2B2C2,并求出平移的距离.
参考答案:
【答案】(1)(0,0);90;(2)画图见解析;平移距离为![]() .
.
【解析】
(1)利用旋转的性质可知,旋转中心在对应点连线的垂直平分线上,分别画AA1、BB1的垂直平分线,交点即为旋转中心;进而可得旋转角;(2)根据A2坐标可知,△ABC向右平移1个单位,向下平移5个单位,据此画出△A2B2C2即可,根据勾股定理求出AA1的长即可得平移距离.
(1)如图:分别连接AA1、BB1,作AA1、BB1的垂直平分线,交点为(0,0),
∴旋转中心为(0,0),∠AOA1为旋转角,
由图像可得∠AOA1=90°,
故答案为:(0,0);90;
(2)∵A(-1,4),A2(0,-1),
∴△ABC向右平移1个单位,向下平移5个单位,
∴△A2B2C2如图所示,
∴AA2=![]() =
=![]() .
.
-
科目: 来源: 题型:
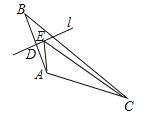
查看答案和解析>>【题目】如图,在△ABC中,点D是AB边的中点,过点D作边AB的垂线l,E是l上任意一点,且AC=5,BC=8,则△AEC的周长最小值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,sin∠BAC=
 ,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为 .
,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题.
已知:如图
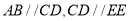 .
.求证:
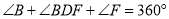
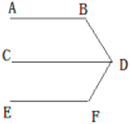
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是_________.
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线
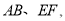 然后在平行线间画了一点
然后在平行线间画了一点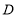 ,连接
,连接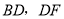 后,用鼠标拖动点分
后,用鼠标拖动点分 别得到了图①②③,小颖发现图②正是上面题目的原型,于是她由上题的结论猜想到图①和③中的
别得到了图①②③,小颖发现图②正是上面题目的原型,于是她由上题的结论猜想到图①和③中的 与
与 之间也可能存在着某种数量关系于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.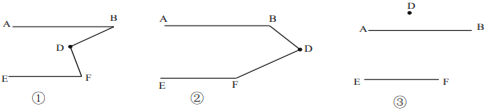
请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图①中
 与
与 之间的数量关系并加以证明:
之间的数量关系并加以证明:②补全图③,直接写出
 与
与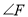 之间的数量关系:_______.
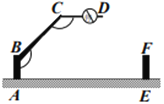
之间的数量关系:_______.(3)学以致用:一个小区大门栏杆的平面示意图如图所示,
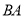 垂直地面
垂直地面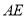 于
于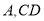 平行于地面
平行于地面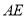 ,若
,若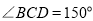 ,则
,则 _______.
_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
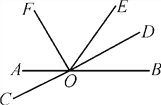
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC. (1)若∠A=36,在△ABC中画一条线段,能得到2个等腰三角形(不包括△ABC),这2个等腰三角形的顶角的度数分别是_____;(2)若∠A≠36, 当∠A=_____时,在等腰△ABC中画一条线段,能得到2个等腰三角形(不包括△ABC).(写出两个答案即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知P、Q是△ABC的BC边上的两点,且BP=AP=AQ=QC,∠PAQ=60°.

(1)求证:AB=AC;
(2)求∠BAC的度数.
相关试题

