【题目】已知在△ABC中,AB=AC. (1)若∠A=36,在△ABC中画一条线段,能得到2个等腰三角形(不包括△ABC),这2个等腰三角形的顶角的度数分别是_____;(2)若∠A≠36, 当∠A=_____时,在等腰△ABC中画一条线段,能得到2个等腰三角形(不包括△ABC).(写出两个答案即可)
参考答案:
【答案】(1)36°,108°; (2)![]() ,90°,108°.
,90°,108°.
【解析】
(1)利用等腰三角形的性质以及∠A的度数,进而得出这2个等腰三角形的顶角度数;
(2)利用(1)种思路进而得出符合题意的图形即可.
(1)如图1所示:∵AB=AC,∠A=36°,∴当AE=BE,则∠A=∠ABE=36°,则∠AEB=108°,则∠EBC=36°,∴这2个等腰三角形的顶角度数分别是36°和108°.
故答案为:36°,108°;
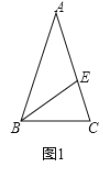
(2)如图1.
∵AB=AC,∴∠ABC=∠C.
∵AD=BD,∴∠ABD=∠A,∴∠BDC=2∠A.
∵BC=DC,∴∠DBC=∠CDB=2∠A,∴∠C=∠ABC=3∠A.
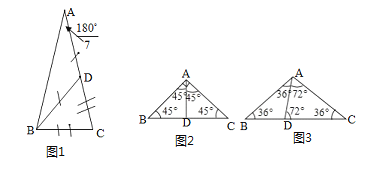
∵∠A+∠ABC+∠C=180°,∴∠A+3∠A+3∠A=180°,∴7∠A=180°∴∠A=![]() .
.
如图2,AB=AC,△ABD和△ADC都是等腰三角形,∠BAC=45°+45°=90°;
如图3,AB=AC,△ABD和△ADC都是等腰三角形,∠BAC=36°+72°=108°.
故答案为:![]() 或90°或108°.
或90°或108°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题.
已知:如图
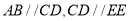 .
.求证:
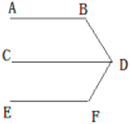
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是_________.
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线
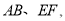 然后在平行线间画了一点
然后在平行线间画了一点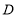 ,连接
,连接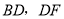 后,用鼠标拖动点分
后,用鼠标拖动点分 别得到了图①②③,小颖发现图②正是上面题目的原型,于是她由上题的结论猜想到图①和③中的
别得到了图①②③,小颖发现图②正是上面题目的原型,于是她由上题的结论猜想到图①和③中的 与
与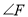 之间也可能存在着某种数量关系于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.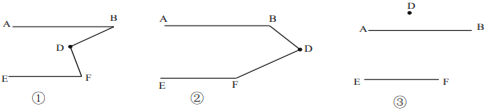
请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图①中
 与
与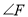 之间的数量关系并加以证明:
之间的数量关系并加以证明:②补全图③,直接写出
 与
与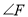 之间的数量关系:_______.
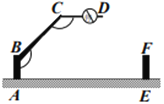
之间的数量关系:_______.(3)学以致用:一个小区大门栏杆的平面示意图如图所示,
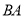 垂直地面
垂直地面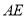 于
于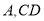 平行于地面
平行于地面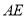 ,若
,若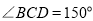 ,则
,则 _______.
_______.
-
科目: 来源: 题型:
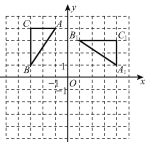
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4),B(-3,1),C(-3,4),△A1B1C1是由△ABC绕某一点旋转得到的.
(1)请直接写出旋转中心的坐标是________,旋转角是_____°;
(2)将△ABC平移得到△A2B2C2,使得点A2的坐标为(0,-1),请画出平移后的△A2B2C2,并求出平移的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
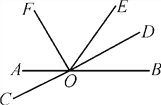
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知P、Q是△ABC的BC边上的两点,且BP=AP=AQ=QC,∠PAQ=60°.

(1)求证:AB=AC;
(2)求∠BAC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
港珠澳大桥是世界上最长的跨海大桥,是被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.开通后从香港到珠海的车程由原来的180千米缩短到50千米,港珠澳大桥的设计时速比按原来路程行驶的平均时速多40千米,若开通后按设计时速行驶,行驶完全程时间仅为原来路程行驶完全程时间的
 ,求港珠澳大桥的设计时速是多少.
,求港珠澳大桥的设计时速是多少.
相关试题

