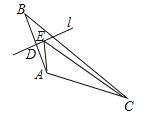
【题目】如图,在△ABC中,点D是AB边的中点,过点D作边AB的垂线l,E是l上任意一点,且AC=5,BC=8,则△AEC的周长最小值为______.
参考答案:
【答案】13
【解析】
连接BE,依据l是AB的垂直平分线,可得AE=BE,进而得到AE+CE=BE+CE,依据BE+CE≥BC,可知当B,E,C在同一直线上时,BE+CE的最小值等于BC的长,而AC长不变,故△AEC的周长最小值等于AC+BC.
如图,连接BE.
∵点D是AB边的中点,l⊥AB,∴l是AB的垂直平分线,∴AE=BE,∴AE+CE=BE+CE.
∵BE+CE≥BC,∴当B,E,C在同一直线上时,BE+CE的最小值等于BC的长,而AC长不变,∴△AEC的周长最小值等于AC+BC=5+8=13.
故答案为:13.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F.
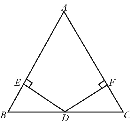
(1)求证;DE=DF;
(2)若∠A=90°,图中与DE相等的还有哪些线段?(不用说明理由)
-
科目: 来源: 题型:
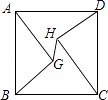
查看答案和解析>>【题目】如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为 .
-
科目: 来源: 题型:
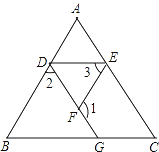
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠B=∠3,你能判断∠C与∠AED的大小关系吗?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,sin∠BAC=
 ,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为 .
,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G,则AG的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题.
已知:如图
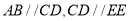 .
.求证:
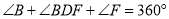
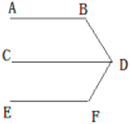
老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是_________.
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线
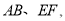 然后在平行线间画了一点
然后在平行线间画了一点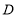 ,连接
,连接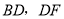 后,用鼠标拖动点分
后,用鼠标拖动点分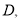 别得到了图①②③,小颖发现图②正是上面题目的原型,于是她由上题的结论猜想到图①和③中的
别得到了图①②③,小颖发现图②正是上面题目的原型,于是她由上题的结论猜想到图①和③中的 与
与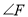 之间也可能存在着某种数量关系于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.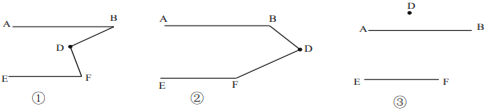
请你在小颖操作探究的基础上,继续完成下面的问题:
①猜想图①中
 与
与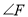 之间的数量关系并加以证明:
之间的数量关系并加以证明:②补全图③,直接写出
 与
与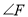 之间的数量关系:_______.
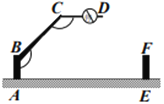
之间的数量关系:_______.(3)学以致用:一个小区大门栏杆的平面示意图如图所示,
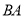 垂直地面
垂直地面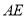 于
于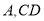 平行于地面
平行于地面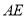 ,若
,若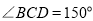 ,则
,则 _______.
_______.
-
科目: 来源: 题型:
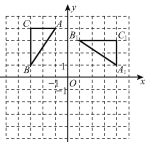
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4),B(-3,1),C(-3,4),△A1B1C1是由△ABC绕某一点旋转得到的.
(1)请直接写出旋转中心的坐标是________,旋转角是_____°;
(2)将△ABC平移得到△A2B2C2,使得点A2的坐标为(0,-1),请画出平移后的△A2B2C2,并求出平移的距离.
相关试题

