【题目】如图,已知P、Q是△ABC的BC边上的两点,且BP=AP=AQ=QC,∠PAQ=60°.

(1)求证:AB=AC;
(2)求∠BAC的度数.
参考答案:
【答案】(1)证明见解析;(2)∠BAC=120°.
【解析】
(1)由AP=AQ,∠PAQ=60°可得△APQ是等边三角形,由BP=AP及外角性质可求出∠B=30°,同理可得∠C=30°,即可证明∠B=∠C,即可得AB=AC;(2)根据三角形内角和定理求出∠BAC的度数即可.
(1)∵AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,∠APQ=∠AQP=60°,
∵BP=AP,
∴∠B=∠BAP,
∵∠APQ=∠B+∠BAP=60°,
∴∠B=30°,
同理可得:∠C=30°,
∴∠B=∠C,
∴AB=AC.
(2)∵∠B=∠C=30°,
∴∠BAC=180°-2∠B=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4),B(-3,1),C(-3,4),△A1B1C1是由△ABC绕某一点旋转得到的.
(1)请直接写出旋转中心的坐标是________,旋转角是_____°;
(2)将△ABC平移得到△A2B2C2,使得点A2的坐标为(0,-1),请画出平移后的△A2B2C2,并求出平移的距离.
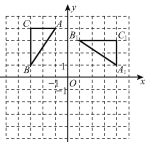
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
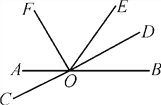
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC. (1)若∠A=36,在△ABC中画一条线段,能得到2个等腰三角形(不包括△ABC),这2个等腰三角形的顶角的度数分别是_____;(2)若∠A≠36, 当∠A=_____时,在等腰△ABC中画一条线段,能得到2个等腰三角形(不包括△ABC).(写出两个答案即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
港珠澳大桥是世界上最长的跨海大桥,是被誉为“现代世界七大奇迹”的超级工程,它是我国从桥梁大国走向桥梁强国的里程碑之作.开通后从香港到珠海的车程由原来的180千米缩短到50千米,港珠澳大桥的设计时速比按原来路程行驶的平均时速多40千米,若开通后按设计时速行驶,行驶完全程时间仅为原来路程行驶完全程时间的
 ,求港珠澳大桥的设计时速是多少.
,求港珠澳大桥的设计时速是多少. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|1﹣
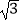 |+3tan30°﹣(
|+3tan30°﹣( 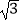 ﹣5)0﹣(﹣
﹣5)0﹣(﹣  )﹣1 .
)﹣1 .
相关试题

