【题目】已知抛物线C1:y=ax2+bx﹣ ![]() (a≠0)经过点A(1,0)和B(﹣3,0).
(a≠0)经过点A(1,0)和B(﹣3,0).
(1)求抛物线C1的解析式,并写出其顶点C的坐标.
(2)如图1,把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2 , 此时点A,C分别平移到点D,E处.设点F在抛物线C1上且在x轴的上方,若△DEF是以EF为底的等腰直角三角形,求点F的坐标.
(3)如图2,在(2)的条件下,设点M是线段BC上一动点,EN⊥EM交直线BF于点N,点P为线段MN的中点,当点M从点B向点C运动时:①tan∠ENM的值如何变化?请说明理由;②点M到达点C时,直接写出点P经过的路线长.
参考答案:
【答案】
(1)解:∵抛物线C1:y=ax2+bx﹣ ![]() (a≠0)经过点A(1,0)和B(﹣3,0),
(a≠0)经过点A(1,0)和B(﹣3,0),
∴ 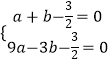 解得
解得 ![]() ,
,
∴抛物线C1的解析式为y= ![]() x2+x﹣
x2+x﹣ ![]() ,
,
∵y= ![]() x2+x﹣
x2+x﹣ ![]() =
= ![]() (x+1)2﹣2,
(x+1)2﹣2,
∴顶点C的坐标为(﹣1,﹣2);
(2)解:如图1,作CH⊥x轴于H,
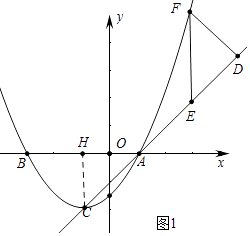
∵A(1,0),C(﹣1,﹣2),
∴AH=CH=2,
∴∠CAB=∠ACH=45°,
∴直线AC的解析式为y=x﹣1,
∵△DEF是以EF为底的等腰直角三角形,
∴∠DEF=45°,
∴∠DEF=∠ACH,
∴EF∥y轴,
∵DE=AC=2 ![]() ,
,
∴EF=4,
设F(m, ![]() m2+m﹣
m2+m﹣ ![]() ),则E(m,m﹣1),
),则E(m,m﹣1),
∴(﹣ ![]() m2+m﹣
m2+m﹣ ![]() )﹣(m﹣1)=4,
)﹣(m﹣1)=4,
解得m=﹣3(舍)或m=3,
∴F(3,6);
(3)解:①tan∠ENM的值为定值,不发生变化;
如图2中,作EG⊥AC,交BF于G,
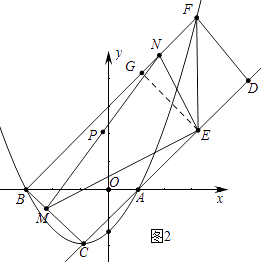
∵DF⊥AC,BC⊥AC,
∴DF∥BC,
∵DF=BC=AC,
∴四边形DFBC是平行四边形,
∵∠CDF=90°,
∴四边形DFBC是矩形,
∴EG=BC=AC=2 ![]() ,
,
∵EN⊥EM,
∴∠MEN=90°,
∵∠CEG=90°,
∴∠CEM=∠NEG,
∴△ENG∽△EMC,
∴ ![]() =
= ![]() ,
,
∵F(3,6),EF=4,
∴E(3,2),
∵C(﹣1,﹣2),
∴EC=4 ![]() ,
,
∴ ![]() =
= ![]() =2,
=2,
∴tan∠ENM= ![]() =2;
=2;
∵tan∠ENM的值为定值,不发生变化;
②如图3﹣1中,
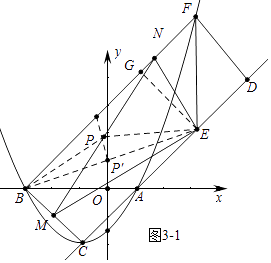
∵直角三角形EMN中,PE= ![]() MN,直角三角形BMN中,PB=
MN,直角三角形BMN中,PB= ![]() MN,
MN,
∴PE=PB,
∴点P在EB的垂直平分线上,
∴点P经过的路径是线段PP′,如图3﹣2,
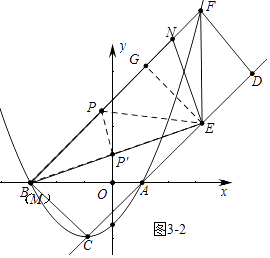
当点M与B重合时,
∵△EGN∽△ECB,
∴ ![]() =
= ![]() ,
,
∵EC=4 ![]() ,EG=BC=2
,EG=BC=2 ![]() ,
,
∴EB=2 ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴EN= ![]() ,
,
∵P1P2是△BEN的中位线,
∴P1P2= ![]() EN=
EN= ![]() ;
;
∴点M到达点C时,点P经过的路线长为 ![]() .
.
【解析】(1)用待定系数法即可求得解析式,把解析式化为顶点式即可求得顶点坐标;(2)根据A、C点的坐标求得直线AC的解析式为y=x﹣1,根据题意的EF=4,求得EF∥y轴,设F(m, ![]() m2+m﹣
m2+m﹣ ![]() ),则E(m,m﹣1),从而得出(﹣
),则E(m,m﹣1),从而得出(﹣ ![]() m2+m﹣
m2+m﹣ ![]() )﹣(m﹣1)=4,解方程即可求得F的坐标;(3)先求得四边形DFBC是平行矩形,作EG⊥AC,交BF于G,然后判断出△ENG∽△EMC,根据相似三角形的性质对应边成比例即可求得tan∠ENM的值,②首先证明点P在EB的垂直平分线上,推出点P经过的路径是线段PP,当点M与B重合时,根据勾股定理和三角形相似求得EN,然后根据三角形中位线定理即可求得。
)﹣(m﹣1)=4,解方程即可求得F的坐标;(3)先求得四边形DFBC是平行矩形,作EG⊥AC,交BF于G,然后判断出△ENG∽△EMC,根据相似三角形的性质对应边成比例即可求得tan∠ENM的值,②首先证明点P在EB的垂直平分线上,推出点P经过的路径是线段PP,当点M与B重合时,根据勾股定理和三角形相似求得EN,然后根据三角形中位线定理即可求得。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:以O为圆心的扇形AOB中,∠AOB=90°,点C为
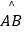 上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.
上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.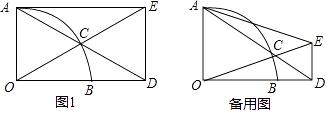
(1)如图1,当四边形AODE为矩形时,求∠ADO的度数;
(2)当扇形的半径长为5,且AC=6时,求线段DE的长;
(3)联结BC,试问:在点C运动的过程中,∠BCD的大小是否确定?若是,请求出它的度数;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有一项工程,甲单独做需要10天能完成,乙单独做需要15天能完成,甲做一天需要的报酬比乙做一天需要的报酬多100元,甲、乙合作完成此项工程需要5400元报酬.
(1)问甲、乙合作多少天能完成此项工程?
(2)求甲做一天需要的报酬;
(3)为了节省开支,应在甲单独完成、乙单独完成、甲乙合作完成这三种方案中选择哪种方案?请通过计算说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.
根据图象信息,以上说法正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A. 2
 B. 6
B. 6 C. 3
C. 3 D.
D. 

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的面积为16cm2,对交线交于点O;以AB、AO为邻边作平行四边AOC1B,对角线交于点O1,以AB、AO1为邻边作平行四边形AO1C2B,…;依此类推,则平行四边形AO4C5B的面积为( )

A.
 cm2 B. 1cm2 C. 2cm2 D. 4cm2
cm2 B. 1cm2 C. 2cm2 D. 4cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
相关试题

