【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A. 2![]() B. 6
B. 6![]() C. 3
C. 3![]() D.
D. ![]()
![]()
参考答案:
【答案】C
【解析】根据矩形的性质和菱形的性质得∠ABE=∠EBD=∠DBC=30°,AB=BO=3,因为四边形BEDF是菱形,所以BE,AE可求出进而可求出BC的长.
解:∵四边形ABCD是矩形,
∴∠A=90°,
即BA⊥BF,
∵四边形BEDF是菱形,
∴EF⊥BD,∠EBO=∠DBF,
∵EF=AE+FC,AE=CF,EO=FO
∴AE=EO=CF=FO,
∴AB=BO=3,∠ABE=∠EBO,
∴∠ABE=∠EBD=∠DBC=30°,
在Rt△BAE中,设AE=x,则BE=2x,由勾股定理得,
∴AB2+AE2=BE2,即32+x2=(2x)2,
BE=2![]() ,
,
∴BF=BE=2![]() ,
,
∴CF=AE=![]() ,
,
∴BC=BF+CF=3![]() ,
,
故选C.
“点睛”本题考查了矩形的性质、菱形的性质以及在直角三角形中30°角所对的直角边时斜边的一半,解题的关键是求出∠ABE=∠EBD=∠DBC=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】泗阳10月3日早上的温度是12℃,中午上升了6℃ ,下午由于冷空气南下,到夜间又下降了7℃,则这天的温差是________℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=2(x+1)2﹣3的图象向右平移2个单位,再向上平移5个单位,可得到抛物线的顶点为( )
A. (﹣3,2) B. (3,8) C. (1,﹣8) D. (1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣4=0的解是( )
A. x=2 B. x1=2,x2=﹣2
C. x1=2,x2=0 D. x=16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是( )

A. 6 B.
 C. 9 D.
C. 9 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A,B在数轴上分别表示有理数
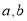 .A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=
.A,B两点之间的距离表示为AB,在数轴上A,B两点之间的距离AB=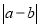 .
.利用数形结合思想回答下列问题:
(1)数轴上表示2和8两点之间的距离是 ;数轴上表示-2和8两点之间的距离是 .
(2)数轴上表示
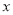 和-4两点A和B之间的距离表示为 ;如果AB=2,那么
和-4两点A和B之间的距离表示为 ;如果AB=2,那么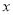 = .
= .(3)若点C表示的数为
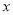 ,当点C在什么位置时,
,当点C在什么位置时, 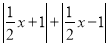 取得的值最小,并直接写出最小值.
取得的值最小,并直接写出最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】xmym+n与2x3y是同类项,那么n等于( )
A.﹣2
B.﹣1
C.0
D.1
相关试题

