【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
参考答案:
【答案】(1)见解析(2)①1;②2
【解析】
试题(1)利用菱形的性质和已知条件可证明四边形AMDN的对边平行且相等即可;
(2)①有(1)可知四边形AMDN是平行四边形,利用有一个角为直角的平行四边形为矩形即∠DMA=90°,所以AM=![]() AD=1时即可;
AD=1时即可;
②当平行四边形AMND的邻边AM=DM时,四边形为菱形,利用已知条件再证明三角形AMD是等边三角形即可.
试题解析:(1)证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME,
又∵点E是AD边的中点,
∴DE=AE,
∴△NDE≌△MAE,
∴ND=MA,
∴四边形AMDN是平行四边形;
(2)解:①当AM的值为1时,四边形AMDN是矩形.理由如下:
∵AM=1=![]() AD,
AD,
∴∠ADM=30°
∵∠DAM=60°,
∴∠AMD=90°,
∴平行四边形AMDN是矩形;
②当AM的值为2时,四边形AMDN是菱形.理由如下:
∵AM=2,
∴AM=AD=2,
∴△AMD是等边三角形,
∴AM=DM,
∴平行四边形AMDN是菱形,
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB为⊙O的直径,CD为⊙O的弦,CD∥AB,过点B的切线与射线AD交于点M,连接AC,BD.
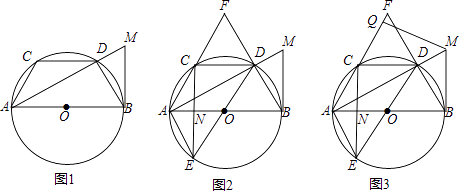
(1)如图l,求证:AC=BD;
(2)如图2,延长AC、BD交于点F,作直径DE,连接AE、CE,CE与AB交于点N,求证:∠AFB=2∠AEN;
(3)如图3,在(2)的条件下,过点M作MQ⊥AF于点Q,若MQ:QC=3:2,NE=2,求QF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在甲乙两家超市发现他看中的一套运动服的单价相同,书包单价也相同.运动服和书包单价之和是452元,且运动服的单价比书包单价的4倍少8元.
(1)求该同学看中的运动服和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,甲超市所有商品打八折销售,乙超市全场每购满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,请说明他能在哪一家购买?若两家都可以选择,在哪一家购买更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,下列说法不正确的是( )
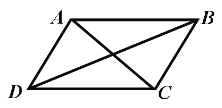
A. 当AC=BD时,四边形ABCD是矩形
B. 当AB=BC时,四边形ABCD是菱形
C. 当AC⊥BD时,四边形ABCD是菱形
D. 当∠DAB=90°时,四边形ABCD是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
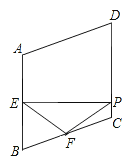
A. 35° B. 45° C. 50° D. 55°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a个单位到△DEF的位置.
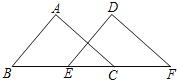
(1)当△ABC所扫过的面积为32时,求a的值;
(2)连接AE、AD,当AB=5,a=5时,试判断△ADE的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=﹣
 (x﹣h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=
(x﹣h)2+k与x轴交于A、B,与y轴交于C,抛物线的顶点为D,对称轴交x轴于H,直线y=  x+
x+  经过点A与对称轴交于E,点E的纵坐标为3.
经过点A与对称轴交于E,点E的纵坐标为3.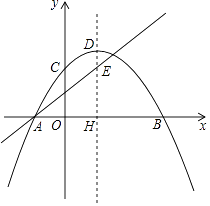
(1)求h、k的值;
(2)点P为第四象限抛物线上一点,连接PH,点Q为PH的中点,连接AQ、AP,设点P的横坐标为t,△AQP的面积为S,求S与t的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,过点Q作y轴的平行线QK,过点D作y轴的垂直DK,直线QK、DK交于点K,连接PK、EK,若2∠DKE+∠HPK=90°,求点P的横坐标.
相关试题

