【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

参考答案:
【答案】(1)此时小强头部E点与地面DK相距约为144.5cm(2)他应向前9.5cm
【解析】试题分析:(1)过点F作FN⊥DK于N,过点E作EM⊥FN于M,利用三角函数求出FM,FN的值即可解决问题,(2)过点E作EP⊥AB于点P,延长OB交MN于N,分别求出OH,PH的值即可做出判断.
(1)如图,过点F作FN⊥DK于N,过点E作EM⊥FN于M.∵EF+FG=166cm,FG=100cm,∴EF=66cm.∵∠FGK=80°,∴FN=100·sin80°≈98cm.
∵∠EFG=125°,∴∠EFM=180°-125°-10°=45°,∴FM=66·cos45°≈46.53cm,∴MN=FN+FM≈144.5cm.∴此时小强头部E点与地面DK相距约为144.5cm.
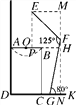
(2)如图,过点E作EP⊥AB于点P,延长OB交MN于H.∵AB=48cm,O为AB中点,∴AO=BO=24cm.∵EM=66·sin45°≈46.53(cm),∴PH≈46.53(cm).
∵GN=100·cos80°≈17(cm),CG=15cm,∴OH=24+15+17=56(cm),OP=OH-PH=56-46.53=9.47≈9.5cm,∴他应向前9.5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
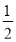 x+b分别交x轴、y轴于点A、C,点P是直线AC与双曲线y=
x+b分别交x轴、y轴于点A、C,点P是直线AC与双曲线y=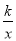 在第一象限内的交点,PB⊥x轴,垂足为点B,且OB=2,PB=4.
在第一象限内的交点,PB⊥x轴,垂足为点B,且OB=2,PB=4.(1)求反比例函数的解析式;
(2)求△APB的面积;
(3)求在第一象限内,当x取何值时一次函数的值小于反比例函数的值?
-
科目: 来源: 题型:
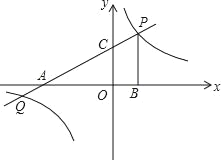
查看答案和解析>>【题目】如图,直线
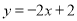 与
与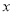 轴、
轴、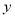 轴分别相交于点A和B.
轴分别相交于点A和B.(1)直接写出坐标:点A ,点B ;
(2)以线段AB为一边在第一象限内作□ABCD,其顶点D(
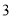 ,
, 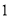 )在双曲线
)在双曲线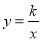 (
(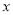 >
>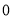 )上.
)上.①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿
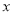 轴向左平移多少个单位长度时,点C恰好落在双曲线
轴向左平移多少个单位长度时,点C恰好落在双曲线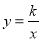 (
(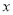 >
>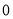 )上.
)上. 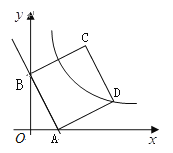
-
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是________(填A或B或C)
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值
②计算:(1-
 )(1-
)(1- )(1-
)(1- )…(1-
)…(1- )(1-
)(1- )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(4,0),B(0,﹣4),C(a,2a)及点D是一个平行四边形的四个顶点,则线段CD的长的最小值为( )
A.
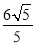 B.
B. 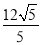 C.
C. 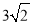 D.
D. 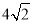
-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图①,∠C=∠ABD=∠E=90°,可知△ACB∽△BED.(不要求证明)
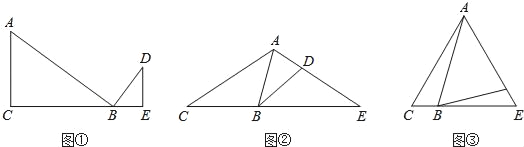
拓展:如图②,∠C=∠ABD=∠E.求证:△ACB∽△BED.
应用:如图③,∠C=∠ABD=∠E=60°,AC=4,BC=1,则△ABD与△BDE的面积比为
.
-
科目: 来源: 题型:
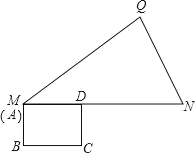
查看答案和解析>>【题目】如图,在△MNQ中,MN=11,NQ=
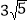 ,
,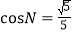 ,矩形ABCD,BC=4,CD=3,点A与M重合,AD与MN重合.矩形ABCD沿着MQ方向平移,且平移速度为每秒5个单位,当点A与Q重合时停止运动.
,矩形ABCD,BC=4,CD=3,点A与M重合,AD与MN重合.矩形ABCD沿着MQ方向平移,且平移速度为每秒5个单位,当点A与Q重合时停止运动.(1)MQ的长度是 ;
(2)运动 秒,BC与MN重合;
(3)设矩形ABCD与△MNQ重叠部分的面积为S,运动时间为t,求出S与t之间的函数关系式.
相关试题

