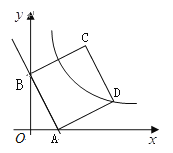
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A和B.
轴分别相交于点A和B.
(1)直接写出坐标:点A ,点B ;
(2)以线段AB为一边在第一象限内作□ABCD,其顶点D(![]() ,
, ![]() )在双曲线
)在双曲线![]() (
(![]() >
>![]() )上.
)上.
①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿![]() 轴向左平移多少个单位长度时,点C恰好落在双曲线
轴向左平移多少个单位长度时,点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.
参考答案:
【答案】(1)A![]() ,B
,B![]() ;(2)①证明见解析②点C恰好落在双曲线
;(2)①证明见解析②点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.
【解析】试题分析:(1)分别令x=0,求出y的值;令y=0,求出x的值即可得出点B与点A的坐标;
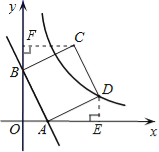
(2)①过点D作DE⊥x轴于点E,由全等三角形的性质可得出△AOB≌△DEA,故可得出AB=AD,再利用待定系数法求出直线AD的解析式即可得出AB⊥AD,由此可得出结论;
②过点C作CF⊥y轴,利用△AOB≌△DEA,同理可得出:△AOB≌△BFC,即可得出C点纵坐标,如果点在图象上,利用纵坐标求出横坐标即可.
解:(1)∵令x=0,则y=2;令y=0,则x=1,
∴A(1,0),B(0,2).
故答案为:(1,0),(0,2);
(2)①过点D作DE⊥x轴于点E,
∵A(1,0),B(0,2),D(3,1),
∴AE=OB=2,OA=DE=1,
在△AOB与△DEA中,
![]() ,
,
∴△AOB≌△DEA(SAS),
∴AB=AD,
设直线AD的解析式为y=kx+b(k≠0),
∴![]() ,
,
解得![]() ,
,
∵(﹣2)×=﹣1,
∴AB⊥AD,
∵四边形ABCD是正方形;
②过点C作CF⊥y轴,
∵△AOB≌△DEA,
∴同理可得出:△AOB≌△BFC,
∴OB=CF=2
∵C点纵坐标为:3,
代入y=,
∴x=1,
∴应该将正方形ABCD沿X轴向左平移2﹣1=1个单位长度时,点C的对应点恰好落在(1)中的双曲线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数y=2x-1,下列说法正确的是( )
A. 它的图象过点(1,0) B. y值随着x值增大而减小
C. 当y>0时,x>1 D. 它的图象不经过第二象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4x2·□=8x3y,则“□”中应填入的代数式是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连结PA,PB.若PB=4,则PA的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC、AD的中点,连接AE、CF.
求证:四边形AECF是矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图.

根据以上信息,解答下列问题:
(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;
(2)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
-
科目: 来源: 题型:
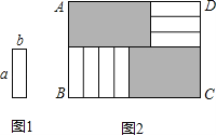
查看答案和解析>>【题目】如图1的7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
A. a=b B. a=2b
C. a=3b D. a=4b
相关试题

