【题目】已知点A,B在数轴上对应的实数分别是a,b,其中a,b满足|a﹣2|+(b+1)2=0.
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程x﹣1=![]() x+1的解,在数轴上是否存在点P,使PA+PB=PC,若存在,求出点P对应的数;若不存在,说明理由;
x+1的解,在数轴上是否存在点P,使PA+PB=PC,若存在,求出点P对应的数;若不存在,说明理由;
(3)在(1)和(2)的条件下,点A,B,C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动,点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,设运动时间为t秒,试探究:随着时间t的变化,AB与BC满足怎样的数量关系?请写出相应的等式.
参考答案:
【答案】(1)3;(2)﹣2或0;(3)t≤![]() 时,AB+BC=7;当t>
时,AB+BC=7;当t>![]() 时,BC﹣AB=7.
时,BC﹣AB=7.
【解析】
(1)根据绝对值及完全平方的非负性,可得出a、b的值,继而可得出线段AB的长;
(2)先求出x的值,再由PA+PB=PC,可得出点P对应的数;
(3)根据A,B,C的运动情况确定AB,BC的变化情况,再根据t的取值范围即可求出AB与BC满足的数量关系.
(1)∵|a﹣2|+(b+1)2=0,∴a=2,b=﹣1,∴线段AB的长为:2﹣(﹣1)=3;
(2)解方程x﹣1=![]() x+1,得x=3,则点C在数轴上对应的数为3.
x+1,得x=3,则点C在数轴上对应的数为3.
![]()
由图知,满足PA+PB=PC时,点P不可能在C点右侧,不可能在线段AC上,①如果点P在点B左侧时,2﹣x+(﹣1)﹣x=3﹣x,解得:x=﹣2;
③当P在A、B之间时,3﹣x=3,解得:x=0.
故所求点P对应的数为﹣2或0;
(3)t秒钟后,A点位置为:2﹣t,B点的位置为:﹣1+4t,C点的位置为:3+9t,BC=3+9t﹣(﹣1+4t)=4+5t,AB=|﹣1+4t﹣2+t|=|5t﹣3|,分两种情况讨论:
①当t≤![]() 时,AB+BC=3﹣5t+4+5t=7;
时,AB+BC=3﹣5t+4+5t=7;
②当t>![]() 时,BC﹣AB=4+5t﹣(5t﹣3)=7.
时,BC﹣AB=4+5t﹣(5t﹣3)=7.
综上所述:当t≤![]() 时,AB+BC=7;当t>
时,AB+BC=7;当t>![]() 时,BC﹣AB=7.
时,BC﹣AB=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】宜宾市开展“创建全国文明城市”活动,城区某校倡议学生利用双休日在“市政广场”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,绘制了不完整的统计图,根据以下图中信息,回答下列问题:

(1)将条形统计图补充完整;
(2)填空:被调查学生劳动时间的众数是______;中位数是________;
(3)求所有被调查同学的平均劳动时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课
A
B
C
D
E
F
人数
20
30
根据图标提供的信息,下列结论错误的是( )
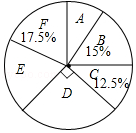
A.这次被调查的学生人数为200人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中最想选F的人数为35人
D.被调查的学生中最想选D的有55人 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在反比例函数y=
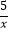 (x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( )
(x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( ) 
A.4.5
B.4.2
C.4
D.3.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )
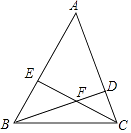
A.20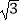
B.25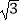
C.30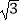
D.40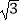
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图像与反比例函数
的图像与反比例函数 的图像交于点
的图像交于点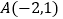 和点
和点 .
.(1)求一次函数和反比例函数的解析式;
(2)直接写出不等式
 的解集;
的解集;(3)若点A关于y轴的对称点为C,问是否在x轴下方存在一点D,使以点A、B、C、D为顶点的四边形是平行四边形.若存在,直接写出点D的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

相关试题

