【题目】如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( ) 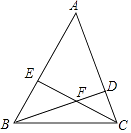
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
参考答案:
【答案】A
【解析】解:连接AF延长AF交BC于G.设EF=CF=x, ∵BD、CE是高,
∴AG⊥BC,
∵∠ABC=60°,∠AGB=90°,
∴∠BAG=30°,
在Rt△AEF中,∵EF=x,∠EAF=30°,∴AE= ![]() x,
x,
在Rt△BCE中,∵EC=2x,∠CBE=60°,∴BE= ![]() x.
x.
∴ ![]() x+
x+ ![]() x=10,
x=10,
∴x=2 ![]() ,
,
∴CE=4 ![]() ,
,
∴S△ABC= ![]() ABCE=
ABCE= ![]() ×10×4
×10×4 ![]() =20
=20 ![]() .
.
故选A.
连接AF延长AF交BC于G.设EF=CF=x,连接AF延长AF交BC于G.设EF=CF=x,因为BD、CE是高,所以AG⊥BC,由∠ABC=60°,∠AGB=90°,推出∠BAG=30°,在Rt△AEF中,由EF=x,∠EAF=30°可得AE= ![]() x,在Rt△BCE中,由EC=2x,∠CBE=60°可得BE=
x,在Rt△BCE中,由EC=2x,∠CBE=60°可得BE= ![]() x.可得
x.可得 ![]() x+
x+ ![]() x=10,解方程即可解决问题.
x=10,解方程即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课
A
B
C
D
E
F
人数
20
30
根据图标提供的信息,下列结论错误的是( )
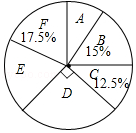
A.这次被调查的学生人数为200人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中最想选F的人数为35人
D.被调查的学生中最想选D的有55人 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在反比例函数y=
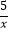 (x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( )
(x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( ) 
A.4.5
B.4.2
C.4
D.3.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B在数轴上对应的实数分别是a,b,其中a,b满足|a﹣2|+(b+1)2=0.
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程x﹣1=
 x+1的解,在数轴上是否存在点P,使PA+PB=PC,若存在,求出点P对应的数;若不存在,说明理由;
x+1的解,在数轴上是否存在点P,使PA+PB=PC,若存在,求出点P对应的数;若不存在,说明理由;(3)在(1)和(2)的条件下,点A,B,C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动,点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,设运动时间为t秒,试探究:随着时间t的变化,AB与BC满足怎样的数量关系?请写出相应的等式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图像与反比例函数
的图像与反比例函数 的图像交于点
的图像交于点 和点
和点 .
.(1)求一次函数和反比例函数的解析式;
(2)直接写出不等式
 的解集;
的解集;(3)若点A关于y轴的对称点为C,问是否在x轴下方存在一点D,使以点A、B、C、D为顶点的四边形是平行四边形.若存在,直接写出点D的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

-
科目: 来源: 题型:
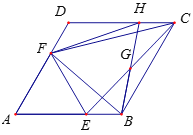
查看答案和解析>>【题目】如图,在菱形ABCD中,
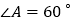 .点E、F分别是边AB、AD上的点,且满足
.点E、F分别是边AB、AD上的点,且满足 ,连结EF.
,连结EF.(1)求证:
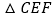 为等腰三角形;
为等腰三角形;(2)若
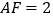 ,求
,求 的面积;
的面积;(3)若G是CE的中点,连结BG并延长交DC于点H,连结FH,求证:
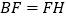 .
. 
相关试题

