【题目】如图，在中，，，，为边上一动点，于，于，为中点，则的最小值为（ ）

A.B.4C.5D.

参考答案：

【答案】D

【解析】

先求证四边形AFPE是矩形，再根据直线外一点到直线上任一点的距离，垂线段最短，利用面积法可求得AP最短时的长，然后即可求出AM最短时的长．

解：连接AP，在△ABC中，AB=6，AC=8，BC=10，


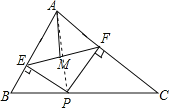
∴∠BAC=90°，
∵PE⊥AB，PF⊥AC，
∴四边形AFPE是矩形，
∴EF=AP．
∵M是EF的中点，
∴AM=AP，
根据直线外一点到直线上任一点的距离，垂线段最短，
即AP⊥BC时，AP最短，同样AM也最短，
∴S△ABC=BCAP＝ABAC，
∴×10AP＝×6×8，
∴AP最短时，AP=，
∴当AM最短时，AM=AP=．
故选：D．

关闭