【题目】如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得到△A′PB.
(1)如图2所示,当PA′⊥BC时,求线段PA的长度.
(2)当∠DPA′=10°时,求∠APB的度数.

参考答案:
【答案】(1)PA=5+5![]() ;(2)85°或95°或5°;
;(2)85°或95°或5°;
【解析】
(1)作BH⊥AD于H.利用特殊直角三角形边角关系 求出AH,BH,即可解决问题.
(2)分情况讨论,求出∠APA′,利用翻折不变性解决问题即可.
解:(1)如图2中,作BH⊥AD于H.
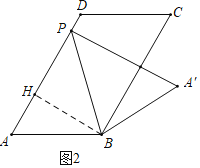
在Rt△ABH中,
∵∠AHB=90°,AB=10,∠A=60°,
∴∠ABH=30°,
∴![]() ,
,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵PA′⊥BC,
∴PA′⊥AD,
∴∠APA′=90°,
∴∠HPB=∠BPA′=45°,
∵BH⊥AD,
∴∠HBP=45°,
∴![]() ,
,
∴![]() ;
;
(2)①如图1-1,
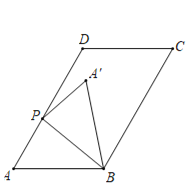
图1-1
当PA′在直线AD的右侧时,
∵∠DPA′=10°,
∴∠APA′=180°﹣∠DPA′=180°﹣10°=170°,
由翻折的性质可知:![]() ;
;
②如图1-2
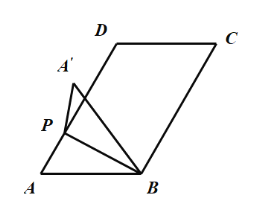
图1-2
当PA′在直线AD的左侧时,由翻折的性质可知:![]() ,
,
③如图1-3
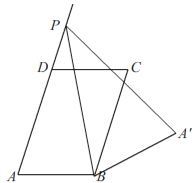
图1-3
当点P在AD的延长线上时,由折叠知,![]() ,
,
故∠APB的度数为85°或95°或5°;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知
 ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”
 ,必有实数根;
,必有实数根;(3)若 x 1是“勾系一元二次方程”
 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6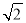 ,求ABC 的面积.
,求ABC 的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:

(1)求扇形统计图中m的值,并补全条形统计图;
(2)在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理? -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数字的许多创新和发展都位居世界前列,如南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”,根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )

A.2019B.2018C.191D.190
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,
, 为边
为边 上一动点,
上一动点, 于
于 ,
, 于
于 ,
, 为
为 中点,则
中点,则 的最小值为( )
的最小值为( )
A.
 B.4C.5D.
B.4C.5D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲船匀速顺流而下从
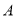 港到
港到 港,同时乙船匀速逆流而上从
港,同时乙船匀速逆流而上从 港到
港到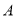 港,
港, 港处于
港处于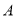 、
、 两港的正中间,某个时刻,甲船接到通知需立即掉头逆流而上到
两港的正中间,某个时刻,甲船接到通知需立即掉头逆流而上到 处,到
处,到 处后迅速按原顺流速度驶向
处后迅速按原顺流速度驶向 港,最后甲、乙两船都到达了各自的目的地.甲、乙两船在静水中的速度相同,设甲、乙两船与
港,最后甲、乙两船都到达了各自的目的地.甲、乙两船在静水中的速度相同,设甲、乙两船与 港的距离之和为
港的距离之和为 ,行驶时间为
,行驶时间为 ,
, 与
与 的部分关系如图,则当两船在
的部分关系如图,则当两船在 、
、 间某处相超时,两船距离
间某处相超时,两船距离 港的距离为________千米.
港的距离为________千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.AO交⊙O于点E,延长AO交⊙O于点D,tanD=
 ,
,
(1)求 的值.
的值.
(2)设⊙O的半径为3,求AB的长.
相关试题

