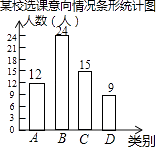
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:
(1)求扇形统计图中m的值,并补全条形统计图;
(2)在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
参考答案:
【答案】
(1)解:总人数=15÷25%=60(人).
A类人数=60﹣24﹣15﹣9=12(人).
∵12÷60=0.2=20%,
∴m=20.
条形统计图如图;
(2)解:抽到选“体育特长类”或“艺术特长类”的学生的概率= ![]() =
= ![]()
(3)解:∵800×25%=200,200÷20=10,
∴开设10个“实验活动类”课程的班级数比较合理
【解析】(1)两个图要结合起来,条形统计图的补全关键是求出所缺部分的数量,部分 ![]() 百分比=总数,具体量=样本容量
百分比=总数,具体量=样本容量![]() 相应百分比;(2)利用概率公式即可;(3)利用“样本的百分比可以估计总体的百分比”,得出结果.
相应百分比;(2)利用概率公式即可;(3)利用“样本的百分比可以估计总体的百分比”,得出结果.
【考点精析】关于本题考查的扇形统计图和条形统计图,需要了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2﹣bx+b(a>0,b>0)图象的顶点的纵坐标不大于
 ,且图象与x轴交于A,B两点,则线段AB长度的最小值是 .
,且图象与x轴交于A,B两点,则线段AB长度的最小值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:二次根式与分式运算
(1)计算:( )﹣2+(
)﹣2+(  ﹣
﹣  )0+(﹣1)1001+(
)0+(﹣1)1001+(  ﹣3
﹣3  )×tan30°
)×tan30°
(2)先化简,再求值: ﹣
﹣  (
(  ﹣a2+b2),其中a=3﹣2
﹣a2+b2),其中a=3﹣2  ,b=3
,b=3  ﹣3.
﹣3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知
 ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”
 ,必有实数根;
,必有实数根;(3)若 x 1是“勾系一元二次方程”
 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6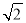 ,求ABC 的面积.
,求ABC 的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数字的许多创新和发展都位居世界前列,如南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”,根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )

A.2019B.2018C.191D.190
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得到△A′PB.
(1)如图2所示,当PA′⊥BC时,求线段PA的长度.
(2)当∠DPA′=10°时,求∠APB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,
, 为边
为边 上一动点,
上一动点, 于
于 ,
, 于
于 ,
, 为
为 中点,则
中点,则 的最小值为( )
的最小值为( )
A.
 B.4C.5D.
B.4C.5D.
相关试题

