【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.AO交⊙O于点E,延长AO交⊙O于点D,tanD= ![]() ,
,
(1)求 ![]() 的值.
的值.
(2)设⊙O的半径为3,求AB的长.
参考答案:
【答案】
(1)解:如图,过点O作OF⊥AB于点F,

∵AO平分∠CAB,
OC⊥AC,OF⊥AB,
∴OC=OF,
∴AB是⊙O的切线;
连接CE,
∵ED是⊙O的直径,
∴∠ECD=90°,
∴∠ECO+∠OCD=90°,
∵∠ACB=90°,
∴∠ACE+∠ECO=90°,
∴∠ACE=∠OCD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ACE=∠ODC,
∵∠CAE=∠CAE,
∴△ACE∽△ADC,
∴ ![]() =
= ![]() ,
,
∵tan∠D= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]()
(2)解:

由(1)可知: ![]() =
= ![]() ,
,
∴设AE=x,AC=2x,
∵△ACE∽△ADC,
∴ ![]() =
= ![]() ,
,
∴AC2=AEAD,
∴(2x)2=x(x+6),
解得:x=2或x=0(不合题意,舍去),
∴AE=2,AC=4,
由(1)可知:AC=AF=4,
∠OFB=∠ACB=90°,
∵∠B=∠B,
∴△OFB∽△ACB,
∴ ![]() =
= ![]() ,
,
设BF=a,
∴BC= ![]() ,
,
∴BO=BC﹣OC= ![]() ﹣3,
﹣3,
在Rt△BOF中,
BO2=OF2+BF2,
∴( ![]() ﹣3)2=32+a2,
﹣3)2=32+a2,
∴解得:a= ![]() 或a=0(不合题意,舍去),
或a=0(不合题意,舍去),
∴AB=AF+BF= ![]() .
.
【解析】(1)可把∠D放在直角三角形中,须连接CE,OF,证出△ACE∽△ADC,利用对应边成比例转化![]() ;(2)利用(1)的结果求出AE、AC,证出△OFB∽△ACB,列出比例式,利用勾股定理建立方程,求出AB.
;(2)利用(1)的结果求出AE、AC,证出△OFB∽△ACB,列出比例式,利用勾股定理建立方程,求出AB.
【考点精析】掌握圆周角定理和相似三角形的判定与性质是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得到△A′PB.
(1)如图2所示,当PA′⊥BC时,求线段PA的长度.
(2)当∠DPA′=10°时,求∠APB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,
, 为边
为边 上一动点,
上一动点, 于
于 ,
, 于
于 ,
, 为
为 中点,则
中点,则 的最小值为( )
的最小值为( )
A.
 B.4C.5D.
B.4C.5D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲船匀速顺流而下从
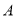 港到
港到 港,同时乙船匀速逆流而上从
港,同时乙船匀速逆流而上从 港到
港到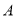 港,
港, 港处于
港处于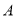 、
、 两港的正中间,某个时刻,甲船接到通知需立即掉头逆流而上到
两港的正中间,某个时刻,甲船接到通知需立即掉头逆流而上到 处,到
处,到 处后迅速按原顺流速度驶向
处后迅速按原顺流速度驶向 港,最后甲、乙两船都到达了各自的目的地.甲、乙两船在静水中的速度相同,设甲、乙两船与
港,最后甲、乙两船都到达了各自的目的地.甲、乙两船在静水中的速度相同,设甲、乙两船与 港的距离之和为
港的距离之和为 ,行驶时间为
,行驶时间为 ,
, 与
与 的部分关系如图,则当两船在
的部分关系如图,则当两船在 、
、 间某处相超时,两船距离
间某处相超时,两船距离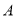 港的距离为________千米.
港的距离为________千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近日天气晴朗,某集团公司准备组织全体员工外出踏青.决定租用甲、乙、丙三种型号的巴士出行,甲型巴士每辆车的乘载量是乙型巴士的3倍,丙型巴士每辆可乘坐36人.现在旅游公司有甲、乙、丙型巴士若干辆,预计给该集团公司安排申型、丙型巴士共计8辆,其余员工安排乙型巴士,每辆巴士均满载,这样乘坐乙型巴士和丙型巴士的员工共296人.临行前,突然有若干人因特殊原因请假,这样一来刚好可以减少租用一辆乙型包士,且有一辆乙型巴士多出两个空位,这样甲、乙两种型号巴士共计装载178人;则该集团公司共有________名员工.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
【答案】B
【解析】解析:∵2a4+2b4+c4=2a2c2+2b2c2,∴4a4-4a2c2+c4+4b4-4b2c2+c4=0,
∴(2a2-c2)2+(2b2-c2)2=0,∴2a2-c2=0,2b2-c2=0,
∴c=2a,c=2b,
∴a=b,且a2+b2=c2,
∴△ABC为等腰直角三角形.
故选B.
【题型】单选题
【结束】
11【题目】将图1中阴影部分的小长方形变换到图2的位置,你能根据两个图形的面积关系得到的数学公式是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A是双曲线y=
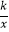 (k>0)在第一象限内的一点,O为坐标原点,直线OA交双曲线于另一点C,当OA在第一象限的角平分线上时,将OA向上平移
(k>0)在第一象限内的一点,O为坐标原点,直线OA交双曲线于另一点C,当OA在第一象限的角平分线上时,将OA向上平移  个单位后,与双曲线在第一象限交于点M,交y轴于点N,若
个单位后,与双曲线在第一象限交于点M,交y轴于点N,若  =2,
=2,
(1)求直线MN的解析式;
(2)求k的值.
相关试题

