搜索
【题目】某工厂为了对新研发的一种产品进行合理定价，将该产品按拟定的价格进行试销，通过对5天的试销情况进行统计，得到如下数据：
单价（元/件） | 25 | 28 | 35 | 40 | 42 |
销量（件） | 50 | 44 | 30 | 20 | 16 |
（1）通过对上面表格中的数据进行分析，发现销量y（件）与单价x（元/件）之间存在一次函数关系，求y关于x的函数关系式（不需要写出函数自变量的取值范围）；
（2）预计在今后的销售中，销量与单价仍然存在（1）中的关系，且该产品的成本是20元/件．为使工厂获得最大利润，该产品的单价应定为多少？
参考答案：
【答案】
（1）解：设一次函数解析式为：y=kx+b，
将（25，50），（28，44）代入函数关系式得：
，
解得： 
，
故一次函数解析式为：y=﹣2x+100；
（2）解：由题意可得：设利润为w
w=（x﹣20）（﹣2x+100）
=﹣2x2+140x﹣2000
=﹣2（x﹣35）2+450，
故产品定价为35元时，工厂获得最大利润．
【解析】（1）利用待定系数法求出一次函数解析式。
（2）根据总利润=每一件的利润
销售量。建立函数关系式，求出其顶点坐标，即可得出答案。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走9m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．
（1）求∠BPQ的度数；
（2）求该电线杆PQ的高度．（结果保留根号） -
科目： 来源： 题型：
查看答案和解析>>【题目】某商店销售
两种商品，每件的售价分别为
元、
元，五一期间，该商店决定对这两种商品进行促销活动，如图所示，若小红打算到该商店购买
件
商品和件
商品，根据以上信息，请：
（1）分别用含的代数式表示按照方案一和方案二所需的费用
和
；（2）就
的不同取值，请说明选择那种方案购买更实惠（两种优惠方案不能同时享受） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点
、
在
的边
上，
，
，（1）求证：
（2）如图2，若
，
，
，求线段
的长
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，PQ为圆O的直径，点B在线段PQ的延长线上，OQ=QB=1，动点A在圆O的上半圆运动（含P、Q两点），
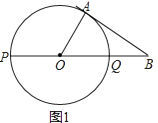
（1）当线段AB所在的直线与圆O相切时，求弧AQ的长（图1）；
（2）若∠AOB=120°，求AB的长（图2）；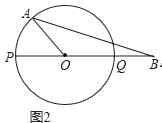
（3）如果线段AB与圆O有两个公共点A、M，当AO⊥PM于点N时，求tan∠MPQ的值（图3）．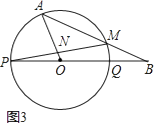
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，等腰
中，
，
为
中点，连接
，
（1）求证：
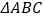是等边三角形（2）如图2，在
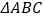内有一点，连接、
、
，若
，求
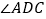的度数（3）如图3，在（2）的条件下，在
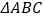外有一点
，连接
、
、若
，
，
，求线段的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，ABCD的顶点的坐标分别为A（﹣6，9），B（0，9），C（3，0），D（﹣3，0），抛物线y=ax2+bx+c（a，b，c为常数，且a≠0）过A、B两点，顶点为M．
（1）若抛物线过点C，求抛物线的解析式；
（2）若抛物线的顶点M落在△ACD的内部（包括边界），求a的取值范围；
（3）若a＜0，连结CM交线段AB于点Q（Q不与点B重合），连接DM交线段AB于点P，设S1=S△ADP+S△CBQ ， S2=S△MPQ ， 试判断S1与S2的大小关系，并说明理由．
相关试题
