【题目】如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走9m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．

（1）求∠BPQ的度数；
（2）求该电线杆PQ的高度．（结果保留根号）

参考答案：

【答案】
（1）解：延长PQ交直线AB于点E，如图所示：

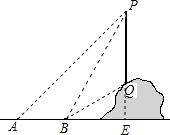
∠BPQ=90°﹣60°=30°；


（2）解：设PE=x米．

在Rt△APE中，∠A=45°，

则AE=PE=x米；

∵∠PBE=60°，

∴∠BPE=30°，

在Rt△BPE中，BE= PE= x米，

∵AB=AE﹣BE=9米，

则x﹣ x=9，

解得：x= ．

则BE= 米．

在直角△BEQ中，QE= BE= 米．

∴PQ=PE﹣QE= ﹣ =9+3 （米）．

答：电线杆PQ的高度为（9+3 ）米．


【解析】（1）延长PQ交直线AB于点E，根据直角三角形两锐角互余求得即可。
（2）设PE=x米，在Rt△APE和Rt△BPE中，根据三角函数利用x表示出AE和BE，根据AB=AE-BE即可列出方程求得x的值，再在Rt△BQE中利用解直角三角形求得QE的长，即可求出PQ的长度。
【考点精析】本题主要考查了特殊角的三角函数值和解直角三角形的相关知识点，需要掌握分母口诀：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口诀：“123，321，三九二十七”；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能正确解答此题．

关闭