【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴的正半轴相交于点A,与y轴相交于点B,点C在线段OA上,点D在此抛物线上,CD⊥x轴,且∠DCB=∠DAB,AB与CD相交于点E.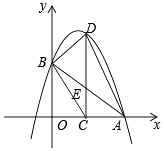
(1)求证:△BDE∽△CAE;
(2)已知OC=2,tan∠DAC=3,求此抛物线的表达式.
参考答案:
【答案】
(1)
证明:∵∠DCB=∠DAB,∠BEC=∠DEA,
∴△BEC∽△DEA,
∴ ![]() =
= ![]() ,又∠BED=∠CEA,
,又∠BED=∠CEA,
∴△BDE∽△CAE;
(2)
解:∵抛物线y=ax2+bx+4与y轴相交于点B,
∴点B的坐标为(0,4),即OB=4,
∵tan∠DAC=3,
∴ ![]() =3,
=3,
设AC=m,则DC=3m,OA=m+2,
则点A的坐标为(m+2,0),点D的坐标为(2,3m),
∵△BDE∽△CAE,
∴∠DBA=∠DCA=90°,
∴BD2+BC2=CD2,即22+(3m﹣4)2+(m+2)2+42=m2+(3m)2,
解得,m=2,
则点A的坐标为(4,0),点D的坐标为(2,6),
∴ ![]() ,
,
解得, ![]() ,
,
∴抛物线的表达式为y=﹣x2+3x+4
【解析】(1)根据相似三角形的判定定理得到△BEC∽△DEA,根据相似三角形的性质定理得到 ![]() =
= ![]() ,根据相似三角形的判定定理证明即可;(2)设AC=m,根据正切的定义得到DC=3m,根据相似三角形的性质得到∠DBA=∠DCA=90°,根据勾股定理列出算式,求出m的值,利用待定系数法求出抛物线的解析式.
,根据相似三角形的判定定理证明即可;(2)设AC=m,根据正切的定义得到DC=3m,根据相似三角形的性质得到∠DBA=∠DCA=90°,根据勾股定理列出算式,求出m的值,利用待定系数法求出抛物线的解析式.
【考点精析】根据题目的已知条件,利用二次函数的概念和二次函数的图象的相关知识可以得到问题的答案,需要掌握一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,第一象限内的点A,B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且cot∠ACB=


求:
(1)反比例函数的解析式;
(2)点C的坐标;
(3)∠ABC的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】将笔记本电脑放置在水平桌面上,显示屏OB与底板OA夹角为115°(如图1),侧面示意图为图2;使用时为了散热,在底板下面垫入散热架O′AC后,电脑转到AO′B′的位置(如图3),侧面示意图为图4,已知OA=0B=20cm,B′O′⊥OA,垂足为C.
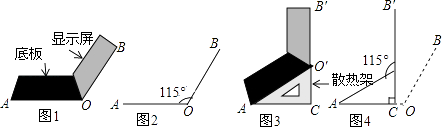
(1)求点O′的高度O′C;(精确到0.1cm)
(2)显示屏的顶部B′比原来升高了多少?(精确到0.1cm)
(3)如图4,要使显示屏O′B′与原来的位置OB平行,显示屏O′B′应绕点O′按顺时针方向旋转多少度? 参考数据:(sin65°=0.906,cos65°=0.423,tan65°=2.146.cot65°=0.446) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,点D,E分别在边AB,BC上,BABD=BCBE

(1)求证:DEAB=ACBE;
(2)如果AC2=ADAB,求证:AE=AC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,AC=BC,点E在DC的延长线上,∠BEC=∠ACB,已知BC=9,cos∠ABC=
 .
.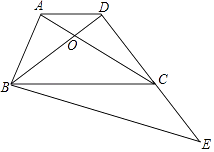
(1)求证:BC2=CDBE;
(2)设AD=x,CE=y,求y与x之间的函数解析式,并写出定义域;
(3)如果△DBC∽△DEB,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于非零向量
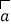 、
、 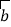 、
、 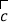 下列条件中,不能判定
下列条件中,不能判定 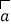 与
与 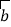 是平行向量的是( )
是平行向量的是( )
A. ∥
∥ 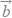 ,
,  ∥
∥ 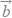
B. +3
+3  =
=  ,
, 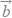 =3
=3 
C. =﹣3
=﹣3 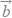
D.| |=3|
|=3| 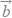 |
| -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=6,AD=3,点P是边AD上的一点,联结BP,将△ABP沿着BP所在直线翻折得到△EBP,点A落在点E处,边BE与边CD相交于点G,如果CG=2DG,那么DP的长是 .

相关试题

