【题目】如图,在矩形ABCD中,AB=6,AD=3,点P是边AD上的一点,联结BP,将△ABP沿着BP所在直线翻折得到△EBP,点A落在点E处,边BE与边CD相交于点G,如果CG=2DG,那么DP的长是 . 
参考答案:
【答案】1
【解析】解:∵CG=2DG,CD=6, ∴CG=4,DG=2,
由勾股定理得,BG= ![]() =5,
=5,
∴EG=1,
由折叠的性质可知,∠E=∠A=90°,又∠EGD=∠CGB,
∴△HEG∽△BCG,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴HG= ![]() ,
,
∴DH=DG﹣HG= ![]() ,
,
同理,DP=1,
所以答案是:1.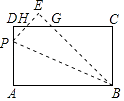
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等),还要掌握翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴的正半轴相交于点A,与y轴相交于点B,点C在线段OA上,点D在此抛物线上,CD⊥x轴,且∠DCB=∠DAB,AB与CD相交于点E.
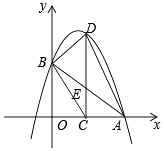
(1)求证:△BDE∽△CAE;
(2)已知OC=2,tan∠DAC=3,求此抛物线的表达式. -
科目: 来源: 题型:
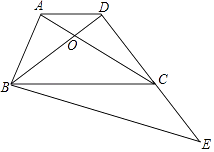
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,AC=BC,点E在DC的延长线上,∠BEC=∠ACB,已知BC=9,cos∠ABC=
 .
.
(1)求证:BC2=CDBE;
(2)设AD=x,CE=y,求y与x之间的函数解析式,并写出定义域;
(3)如果△DBC∽△DEB,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于非零向量
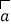 、
、 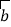 、
、 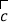 下列条件中,不能判定
下列条件中,不能判定 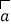 与
与 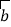 是平行向量的是( )
是平行向量的是( )
A. ∥
∥ 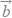 ,
,  ∥
∥ 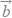
B. +3
+3  =
=  ,
, 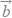 =3
=3 
C. =﹣3
=﹣3 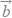
D.| |=3|
|=3| 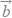 |
| -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x
…
﹣1
0
2
3
4
…
y
…
5
2
2
5
10
…
(1)根据上表填空: ①这个抛物线的对称轴是 , 抛物线一定会经过点(﹣2,);
②抛物线在对称轴右侧部分是(填“上升”或“下降”);
(2)如果将这个抛物线y=ax2+bx+c向上平移使它经过点(0,5),求平移后的抛物线表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,过点A作AD⊥BC,垂足为点D,延长AD至点E,使DE=
 AD,过点A作AF∥BC,交EC的延长线于点F.
AD,过点A作AF∥BC,交EC的延长线于点F. 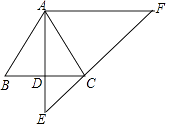
(1)设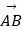 =
= 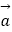 ,
, 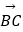 =
= 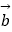 ,用
,用 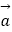 、
、 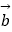 的线性组合表示
的线性组合表示 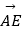 ;
;
(2)求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图(图2),支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得DE=20厘米,DC=40厘米,∠AED=58°,∠ADE=76°.
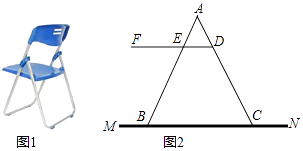
(1)求椅子的高度(即椅子的座板DF与地面MN之间的距离)(精确到1厘米)
(2)求椅子两脚B、C之间的距离(精确到1厘米)(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin76°≈0.97.cos76°≈0.24,tan76°≈4.00)
相关试题

