【题目】某校决定在4月7日开展“世界无烟日”宣传活动,活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了两种不完整的统计图表:
选项 | 方式 | 百分比 |
A | 社区板报 | 35% |
B | 集会演讲 | m |
C | 喇叭广播 | 25% |
D | 发宣传画 | 10% |
请结合统计图表,回答下列问题:
(1)本次抽查的学生共人,m= , 并将条形统计图补充完整;
(2)若该校学生有1500人,请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四种宣传方式在随机抽取两种进行展示,请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率.
参考答案:
【答案】
(1)300,30%解:补全条形图如下:
(2)解:1500×30%=450(人),
答:估计该校喜欢“集会演讲”这项宣传方式的学生约有450人
(3)解:画树状图为:

共有12种等可能的结果数,其中所抽到的两项方式恰好是“集会演讲”和“喇叭广播”的结果数为2,
∴所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率为 ![]() =
= ![]()
【解析】解:(1)本次调查的学生共有105÷35%=300(人),m=1﹣(35%+25%+10%)=30%,
B项目的人数为:300×30%=90(人),
补全条形图如下:

所以答案是:300,30%;
【考点精析】解答此题的关键在于理解统计表的相关知识,掌握制作统计表的步骤:(1)收集整理数据.(2)确定统计表的格式和栏目数量,根据纸张大小制成表格.(3)填写栏目、各项目名称及数据.(4)计算总计和合计并填入表中,一般总计放在横栏最左格,合计放在竖栏最上格.(5)写好表格名称并标明制表时间,以及对条形统计图的理解,了解能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A﹣C﹣B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C﹣B﹣A向A点运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t=秒时,△PCQ的面积等于8cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点在第一,四象限及x轴上运动,在第1次,它从原点运动到点(1,﹣1),用了1秒,然后按图中箭头所示方向运动,即(0,0)→(1,﹣1)→(2,0)→(3,1)→…,它每运动一次需要1秒,那么第2020秒时点所在的位置的坐标是__.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请完成下面的解答过程完.如图,∠1=∠B,∠C=110°,求∠3的度数.

解:∵∠1=∠B
∴AD∥( )(内错角相等,两直线平行)
∴∠C+∠2=180°,( )
∵∠C=110°.
∴∠2=( )°.
∴∠3=∠2=70°.( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:
 ;
;(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,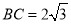 ,
, ,
, 、
、 分别是
分别是 、
、 上的点,且
上的点,且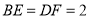 ,连结
,连结 、
、 .点
.点 是线段
是线段 上的点,过点
上的点,过点 作
作 交
交 于点
于点 ,设AP=x.
,设AP=x.
(1)求证:四边形
 是菱形;
是菱形;(2)用含
 的代数式表示
的代数式表示 的长;
的长;(3)连结
 ,当
,当 为何值时
为何值时 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 ;
(2)线段CD由线段AB经过怎样平移得到?
(3)求F的坐标.

相关试题

