【题目】如图,在平面直角坐标系中,点A(0,5),B(﹣2,0),C(3,3),线段AB经过平移得到线段CD,其中点B的对应点为点C,点D在第一象限,直线AC交x轴于点F.
(1)点D坐标为 ;
(2)线段CD由线段AB经过怎样平移得到?
(3)求F的坐标.

参考答案:
【答案】(1)(5,8);(2)向右平移5个单位,再向上平移3个单位;(3)F(![]() ,0).
,0).
【解析】
(1)根据点B移动到A的平移规律可得结论.
(2)根据点B移动到A的平移规律可得结论.
(3)作CH⊥OF于H.设F(m,0),根据S△AOF=S四边形AOHC+S△CHF,列出方程求出m的值.
解:(1)∵点B向右平移2个单位,再向上平移5个单位得到点A,
∴点C(3,3)向右平移2个单位,再向上平移5个单位得到点D(5,8).
故答案为(5,8).
(2)向右平移5个单位,再向上平移3个单位
(3)作CH⊥OF于H.设F(m,0).
∵S△AOF=S四边形AOHC+S△CHF,
∴![]() ×5×m=
×5×m=![]() ×(3+5)×3+
×(3+5)×3+![]() ×3×(m﹣3),
×3×(m﹣3),
解得:m=![]() ,∴F(
,∴F(![]() ,0),
,0),
(也可连接OC,再利用面积求)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校决定在4月7日开展“世界无烟日”宣传活动,活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了两种不完整的统计图表:
选项
方式
百分比
A
社区板报
35%
B
集会演讲
m
C
喇叭广播
25%
D
发宣传画
10%
请结合统计图表,回答下列问题:

(1)本次抽查的学生共人,m= , 并将条形统计图补充完整;
(2)若该校学生有1500人,请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四种宣传方式在随机抽取两种进行展示,请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,将两个边长为1的小正方形分别沿对角线剪开,拼成正方形ABCD.
(1)正方形ABCD的面积为 ,边长为 ,对角线BD= ;
(2)求证:
 ;
;(3)如图②,将正方形ABCD放在数轴上,使点B与原点O重合,边AB落在x轴的负半轴上,则点A所表示的数为 ,若点E所表示的数为整数,则点E所表示的数为 .


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,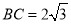 ,
, ,
, 、
、 分别是
分别是 、
、 上的点,且
上的点,且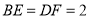 ,连结
,连结 、
、 .点
.点 是线段
是线段 上的点,过点
上的点,过点 作
作 交
交 于点
于点 ,设AP=x.
,设AP=x.
(1)求证:四边形
 是菱形;
是菱形;(2)用含
 的代数式表示
的代数式表示 的长;
的长;(3)连结
 ,当
,当 为何值时
为何值时 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )
A.

B.

C.

D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,求∠HPQ的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据语句画图,并回答问题,如图,∠AOB内有一点P.
(1)过点P画PC∥OB交OA于点C,画PD∥OA交OB于点D.
(2)写出图中与∠CPD互补的角 .(写两个即可)
(3)写出图中∠O相等的角 .(写两个即可)

相关试题

