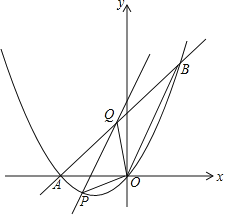
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于原点及点A,且经过点B(4,8),对称轴为直线x=﹣2.
(1)求抛物线的解析式;
(2)设直线y=kx+4与抛物线两交点的横坐标分别为x1,x2(x1<x2),当![]() 时,求k的值;
时,求k的值;
(3)连接OB,点P为x轴下方抛物线上一动点,过点P作OB的平行线交直线AB于点Q,当S△POQ:S△BOQ=1:2时,求出点P的坐标.
(坐标平面内两点M(x1,y1),N(x2,y2)之间的距离MN=![]() )
)
参考答案:
【答案】(1)抛物线解析式为y=![]() x2+x;(2)k=1;(3)P(﹣2
x2+x;(2)k=1;(3)P(﹣2![]() ,﹣2
,﹣2![]() +2).
+2).
【解析】(1)先利用对称轴公式得出b=4a,进而利用待定系数法即可得出结论;
(2)先利用根与系数的关系得出,x1+x2=4(k﹣1),x1x2=﹣16,转化已知条件,代入即可得出结论;
(3)先判断出OB=2PQ,进而判断出点C是OB中点,再求出AB解析式,判断出PC∥AB,即可得出PC解析式,和抛物线解析式联立解方程组即可得出结论.
(1)根据题意得,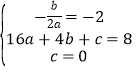 ,
,
∴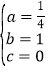 ,
,
∴抛物线解析式为y=![]() x2+x;
x2+x;
(2)∵直线y=kx+4与抛物线两交点的横坐标分别为x1,x2,
∴![]() x2+x=kx+4,
x2+x=kx+4,
∴x2﹣4(k﹣1)x﹣16=0,
根据根与系数的关系得,x1+x2=4(k﹣1),x1x2=﹣16,
∵![]() ,
,
∴2(x1﹣x2)=x1x2,
∴4(x1﹣x2)2=(x1x2)2,
∴4[(x1+x2)2﹣4x1x2]=(x1x2)2,
∴4[16(k﹣1)2+64]=162,
∴k=1;
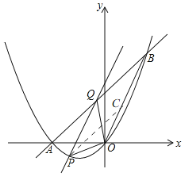
(3)如图,取OB的中点C,
∴BC=![]() OB,
OB,
∵B(4,8),
∴C(2,4),
∵PQ∥OB,
∴点O到PQ的距离等于点O到OB的距离,
∵S△POQ:S△BOQ=1:2,
∴OB=2PQ,
∴PQ=BC,∵PQ∥OB,
∴四边形BCPQ是平行四边形,
∴PC∥AB,
∵抛物线的解析式为y=![]() x2+x①,
x2+x①,
令y=0,
∴![]() x2+x=0,
x2+x=0,
∴x=0或x=﹣4,
∴A(﹣4,0),
∵B(4,8),
∴直线AB解析式为y=x+4,设直线PC的解析式为y=x+m,
∵C(2,4),
∴直线PC的解析式为y=x+2②,
联立①②解得,![]() (舍)或
(舍)或![]() ,
,
∴P(﹣2![]() ,﹣2
,﹣2![]() +2).
+2).
-
科目: 来源: 题型:
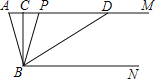
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C为⊙O上一点,经过点C的切线交AB的延长线于点E,AD⊥EC交EC的延长线于点D,AD交⊙O于F,FM⊥AB于H,分别交⊙O、AC于M、N,连接MB,BC.
(1)求证:AC平分∠DAE;
(2)若cosM=
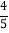 ,BE=1,①求⊙O的半径;②求FN的长.
,BE=1,①求⊙O的半径;②求FN的长.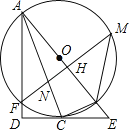
-
科目: 来源: 题型:
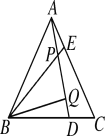
查看答案和解析>>【题目】如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:△ABE≌△CAD;
(2) 求BE的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】在第23个世界读书日前夕,我市某中学为了解本校学生的每周课外阅读时间
 用t表示,单位:小时
用t表示,单位:小时 ,采用随机抽样的方法进行问卷调查,调查结果按
,采用随机抽样的方法进行问卷调查,调查结果按 ,
, ,
, ,
, 分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
 求本次调查的学生人数;
求本次调查的学生人数; 求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整; 若该校共有学生1200人,试估计每周课外阅读时间满足
若该校共有学生1200人,试估计每周课外阅读时间满足 的人数.
的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用相同的小正方形按照某种规律进行摆放.根据图中小正方形的排列规律,猜想第
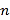 个图中小正方形的个数为___________(用含
个图中小正方形的个数为___________(用含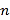 的式子表示)
的式子表示)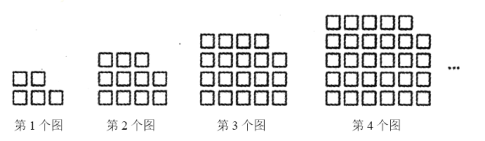
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC中,点D在BC边上(不与点B、点C重合),点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②若点D在BC边上运动,DA与AM始终相等吗?请说明理由.

相关试题

