【题目】在第23个世界读书日前夕,我市某中学为了解本校学生的每周课外阅读时间![]() 用t表示,单位:小时
用t表示,单位:小时![]() ,采用随机抽样的方法进行问卷调查,调查结果按
,采用随机抽样的方法进行问卷调查,调查结果按![]() ,
,![]() ,
,![]() ,
,![]() 分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

![]() 求本次调查的学生人数;
求本次调查的学生人数;
![]() 求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
![]() 若该校共有学生1200人,试估计每周课外阅读时间满足
若该校共有学生1200人,试估计每周课外阅读时间满足![]() 的人数.
的人数.
参考答案:
【答案】![]() 本次调查的学生人数为200人;
本次调查的学生人数为200人;![]() B所在扇形的圆心角为
B所在扇形的圆心角为![]() ,补全条形图见解析;
,补全条形图见解析;![]() 全校每周课外阅读时间满足
全校每周课外阅读时间满足![]() 的约有360人.
的约有360人.
【解析】![]() 根据等级A的人数及所占百分比即可得出调查学生人数;
根据等级A的人数及所占百分比即可得出调查学生人数;
![]() 先计算出C在扇形图中的百分比,用
先计算出C在扇形图中的百分比,用![]() 在扇形图中的百分比
在扇形图中的百分比![]() 可计算出B在扇形图中的百分比,再计算出B在扇形的圆心角;
可计算出B在扇形图中的百分比,再计算出B在扇形的圆心角;
![]() 总人数
总人数![]() 课外阅读时间满足
课外阅读时间满足![]() 的百分比即得所求.
的百分比即得所求.
![]() 由条形图知,A级的人数为20人,
由条形图知,A级的人数为20人,
由扇形图知:A级人数占总调查人数的![]() ,
,
所以:![]() 人
人![]() ,
,
即本次调查的学生人数为200人;
![]() 由条形图知:C级的人数为60人,
由条形图知:C级的人数为60人,
所以C级所占的百分比为:![]() ,
,
B级所占的百分比为:![]() ,
,
B级的人数为![]() 人
人![]() ,
,
D级的人数为:![]() 人
人![]() ,
,
B所在扇形的圆心角为:![]() ,
,
补全条形图如图所示:
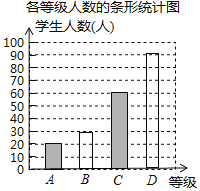 ;
;
![]() 因为C级所占的百分比为
因为C级所占的百分比为![]() ,
,
所以全校每周课外阅读时间满足![]() 的人数为:
的人数为:![]() 人
人![]() ,
,
答:全校每周课外阅读时间满足![]() 的约有360人.
的约有360人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)求值:

(2)用消元法解方程组
 时,两位同学的解法如下:
时,两位同学的解法如下:解法一:
由①-②,得
 .
.解法二:
由②得,
 ,③
,③把①代入③,得
 .
.①反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“×”.
②请选择一种你喜欢的方法,完成解答.
(3)求不等式组
 的正整数解.
的正整数解. -
科目: 来源: 题型:
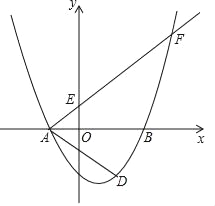
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知抛物线y=
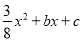 与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且
与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且 .
.(1)求这条抛物线的表达式,并写出它的对称轴;
(2)求∠FAB的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长均为1个单位的正方形网格图中,建立了平面直角坐标系xOy,按要求解答下列问题:

(1)写出△ABC三个顶点的坐标;
(2)画出△ABC向右平移6个单位后得到的图形△A1B1C1;
(3)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J. Nplcr,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707-1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若
 ,那么
,那么 叫做以
叫做以 为底
为底 的对数,记作:
的对数,记作: .比如指数式
.比如指数式 可以转化为
可以转化为 ,对数式
,对数式 可以转化为
可以转化为 .
.我们根据对数的定义可得到对数的一个性质:
 ;理由如下:
;理由如下:设
 ,
, ,则
,则 ,
,
∴
 ,由对数的定义得
,由对数的定义得
又∵

∴

解决以下问题:
(1)将指数
 转化为对数式______;
转化为对数式______;(2)证明

(3)拓展运用:计算
 ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设
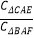 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是
 时,求AB的长.
时,求AB的长.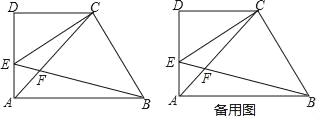
相关试题

