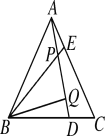
【题目】如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:△ABE≌△CAD;
(2) 求BE的长
参考答案:
【答案】(1)证明见解析;(2)7
【解析】
(1)根据AE=CD,AB=AC,∠BAC=∠C即可求得△ABE≌△CAD;
(2)由(1)得∠AEB=∠ADC,即可求得∠BPQ=∠C,即可求得BP的长,即可解题.
(1)∵△ABC是等边三角形,
∴AB=BC=AC,
∴∠BAC=∠C=60°,
∵AB=AC,AE=CD,
∴△ADC≌△BEA,
(2)∵△ADC≌△BEA,
∴∠ABE=∠CAD,
∵∠CAD+∠BAD=60°,
∴∠ABE+∠BAD=60°,
∴∠BPQ=60°,
∵BQ⊥AD,
∴∠PBQ=30°,
∴BP=2PQ,
∴BP=6,
∴BE=BP+PE=6+1=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】首都国际机场连续五年排名全球最繁忙机场第二位,该机场2012﹣2016年客流量统计结果如表:
年份
2012
2013
2014
2015
2016
客流量(万人次)
8192
8371
8613
8994
9400
根据统计表中提供的信息,预估首都国际机场2017年客流量约万人次,你的预估理由是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:6sin60°﹣(
 )﹣2﹣
)﹣2﹣ 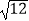 +|2﹣
+|2﹣  |.
|. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
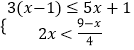 并写出它的所有整数解.
并写出它的所有整数解. -
科目: 来源: 题型:
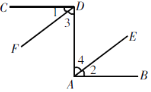
查看答案和解析>>【题目】如图,已知CD⊥DA,DA⊥AB,∠1=∠2. 试说明DF∥AE. 请你完成下列填空,把解答过程补充完整.
解:∵CD⊥DA,DA⊥AB,
∴∠CDA=90°,∠DAB=90°( ).
∴∠CDA=∠DAB(等量代换).
又∠1=∠2,
从而∠CDA-∠1=∠DAB-________(等式的性质).
即∠3=_______.
∴DF∥AE( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把直角三角形纸片沿过顶点B的直线(BE交CA于E)折叠,直角顶点C落在斜边AB上,如果折叠后得等腰△EBA,那么结论中:①∠A=30°;②点C与AB的中点重合;③点E到AB的距离等于CE的长,正确的个数是( )
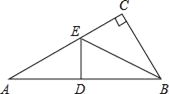
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程mx2﹣(2m﹣3)x+(m﹣1)=0有两个实数根.
(1)求m的取值范围;
(2)若m为正整数,求此方程的根.
相关试题

