【题目】在等边△ABC中,点D在BC边上(不与点B、点C重合),点E在AC的延长线上,DE=DA(如图1).
(1)求证:∠BAD=∠EDC;
(2)点E关于直线BC的对称点为M,连接DM,AM.
①依题意将图2补全;
②若点D在BC边上运动,DA与AM始终相等吗?请说明理由.

参考答案:
【答案】证明见解析
【解析】
(1)因为DE=DA,,根据等边对等角可得:∠E=∠DAC,由△ABC是等边三角形,可得∠BAC=∠ACD=60°,即∠BAD+∠DAC=∠E+∠EDC=60°,进而可得:∠BAD=∠EDC,
(2)②证法1:由轴对称可得,DM=DE,∠EDC=∠MDC,
由DE=DA,可得:DM=DA,由(1)可得,∠BAD=∠EDC,等量代换可得:∠MDC=∠BAD,
因为在△ABD中,∠BAD+∠ADB=180°﹣∠B=120°,可证得:∠MDC+∠ADB=120°,继而可得:
∠ADM=180°﹣120°=60°,可得:△ADN是等边三角形,所以AD=AM,
证法2:连接CM,由轴对称可得,DM=DE,∠EDC=∠MDC,
由DE=DA,等量代换可得:DM=DA,由(1)可得,∠BAD=∠EDC,等量代换可得:
∠MDC=∠BAD,因为在△ABD中,∠BAD+∠ADB=180°﹣∠B=120°,
可得:∠MDC+∠ADB=120°,进而可得:∠ADM=180°﹣120°=60°,故△ADM中,∠DAM=(180°﹣60°)÷2=60°,根据∠BAC=60°,可得∠BAD=∠CAM,由轴对称可得,∠DCE=∠DCM=120°,
又因为∠ACB=60°,所以∠ACM=120°﹣60°=60°,即∠B=∠ACM,
在△ABD和△ACM中,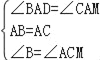 ,可判定△ABD≌△ACM(ASA),所以AD=AM.
,可判定△ABD≌△ACM(ASA),所以AD=AM.
(1)如图1,
∵DE=DA,
∴∠E=∠DAC,
∵△ABC是等边三角形,
∴∠BAC=∠ACD=60°,
即∠BAD+∠DAC=∠E+∠EDC=60°,
∴∠BAD=∠EDC,
(2)①补全图形如图2,
②证法1:由轴对称可得,DM=DE,∠EDC=∠MDC,
∵DE=DA,
∴DM=DA,
由(1)可得,∠BAD=∠EDC,
∴∠MDC=∠BAD,
∵△ABD中,∠BAD+∠ADB=180°﹣∠B=120°,
∴∠MDC+∠ADB=120°,
∴∠ADM=180°﹣120°=60°,
∴△ADN是等边三角形,
∴AD=AM,
证法2:连接CM,
由轴对称可得,DM=DE,∠EDC=∠MDC,
∵DE=DA,
∴DM=DA,
由(1)可得,∠BAD=∠EDC,
∴∠MDC=∠BAD,
∵△ABD中,∠BAD+∠ADB=180°﹣∠B=120°,
∴∠MDC+∠ADB=120°,
∴∠ADM=180°﹣120°=60°,
∴△ADM中,∠DAM=(180°﹣60°)÷2=60°,
又∵∠BAC=60°,
∴∠BAD=∠CAM,
由轴对称可得,∠DCE=∠DCM=120°,
又∵∠ACB=60°,
∴∠ACM=120°﹣60°=60°,
∴∠B=∠ACM,
在△ABD和△ACM中,
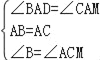 ,
,
∴△ABD≌△ACM(ASA),
∴AD=AM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.
(1)求这个多边形是几边形;
(2)求这个多边形的每一个内角的度数.
-
科目: 来源: 题型:
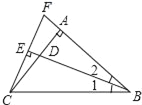
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.CE=2,延长CE,BA交于点F.
(1)求证:△ADB≌△AFC;
(2)求BD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】桐梓县“四抓四到位”确保教育均衡发展,加速城区新、扩建项目工程,加快建设某间小学,公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的2倍,甲、乙两队合作完成建校工程需要60天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)若甲、乙两队共同工作了10天后,乙队因其他工作停止施工,由甲队单独继续施工,要使甲队总的工作量不少于乙队已做工作量的2倍,那么甲队至少再单独施工多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.
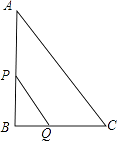
(1)用含x的代数式表示BQ、BP的长度,并求x的取值范围.
(2)设四边形APQC的面积为y(cm2),求y与x的函数关系式?
(3)是否存在这样的x,使得四边形APQC的面积是△ABC面积的 ?如果存在,求出x的值;不存在请说明理由.
?如果存在,求出x的值;不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式
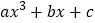 ,当
,当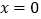 时,该代数式的值为3.
时,该代数式的值为3.(1)求c的值;
(2)已知:当
 时,该代数式的值为0.
时,该代数式的值为0.①求:当
 时,该代数式的值;
时,该代数式的值;②若
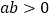 ,
, ,
, ,试比较a与d的大小,并说明理由.
,试比较a与d的大小,并说明理由.
相关试题

